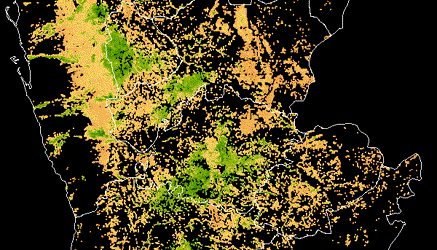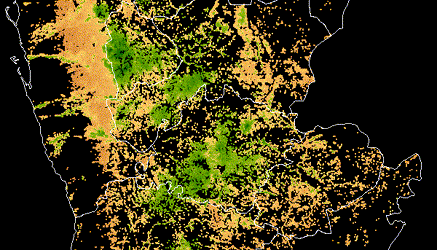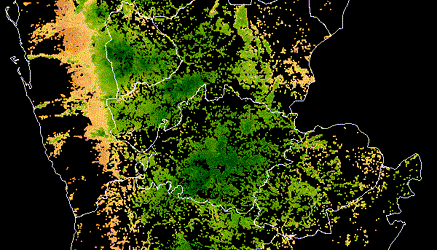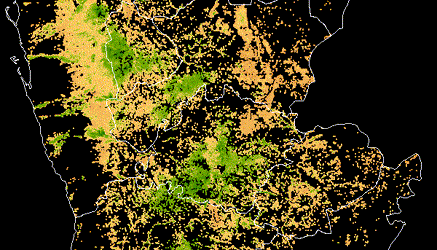
Differential Privacy Temporal Map Challenge¶
Large data sets containing personally identifiable information (PII) are exceptionally valuable resources for research and policy analysis in a host of fields supporting America's First Responders such as emergency planning and epidemiology.
Temporal map data is of particular interest to the public safety community in applications such as optimizing response time and personnel placement, natural disaster response, epidemic tracking, demographic data and civic planning. Yet, the ability to track information related to a person's location over a period of time presents particularly serious privacy concerns.
The goal of the Differential Privacy Temporal Map Challenge (DeID2) is to develop algorithms that preserve data utility as much as possible while guaranteeing individual privacy is protected. The challenge features a series of coding sprints to apply differential privacy methods to temporal map data, where one individual in the data may contribute to a sequence of events.
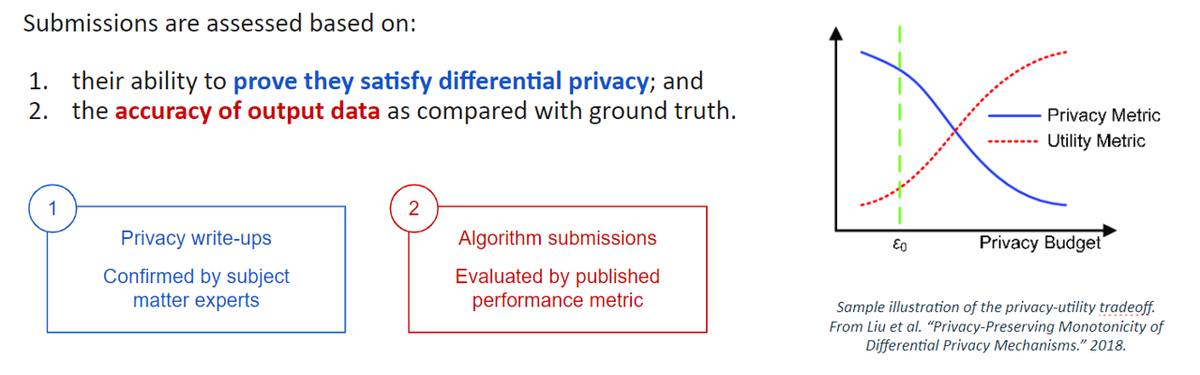
Sprint 2: American Community Survey (ACS)¶
Sprint 2 was open to submissions from January 6th to February 22, 2021. This sprint featured census data about simulated individuals in various US states from 2012-2018, including 35 different survey features aside from the simulated individual the record belonged to. These individual records were also linked across years, increasing the challenge to make sure each person's privacy was protected. To succeed in this competition, participants needed to build de-identification algorithms generating a set of synthetic, privatized survey records that most accurately preserved the patterns in the original data.
While the third sprint of the 2018-2019 NIST Differential Privacy Synthetic Data Challenge (DeID1) dealt with a related U.S. Census data problem, the temporal map challenge introduces new complications by allowing one individual to contribute multiple records (up to 7 in this sprint). This increases the sensitivity of many queries, and thus increases the amount of added noise necessary to guarantee privacy. Additionally, because accuracy is evaluated with respect to all map segments (Public Use Microdata Areas) and time segments (years), it was important that solutions provide good performance even on the more complex or sparse sections of the data.
Winning competitors found that general techniques which had proven effective in the 2018-2019 Synthetic Data challenge were also useful here, although advances were necessary to address the difficulties imposed by the temporal map context.
- Probabilistic Graphical Models (PGM): Both N-CRiPT and Minutemen used PGM-based approaches, which were also used by the first place winner of the 2018-2019 challenge. Each team tailored their approach and applied new techniques to deal with the increased sensitivity of the temporal data.
- Noisy Marginals: On the high epsilon setting, both DukeDP and DPSyn used approaches which first collected a set of marginal counts from the data, then privatized the counts with added noise, and finally used post-processing and sampling from the public data to produce a final consistent synthetic data set. DPSyn also used a similar technique when they earned second place in the 2018-2019 challenge. Each team introduced new strategies to handle the increased difficulty of the problem, including new approaches to creating the final consistent data.
- Histograms: In the 2018-2019 challenge, the DPFields solution partitioned the variables in the schema and then collected (and privatized) histograms over each of the partitions, and finally used these noisy histograms as probability distributions for sampling the synthetic data. Jim King used a similar approach, carefully tailoring the choice of histograms and level of aggregation to the more challenging temporal map problem.
These solutions were evaluated based on scores of data utility at different levels of guaranteed privacy (indicated by epsilon). In this sprint, solutions were evaluated using the "K-marginal Evaluation Metric". The K-marginal metric was developed for the 2018-2019 challenge and is designed to measure how faithfully each privatization algorithm preserves the most significant patterns across all features in the data within each map/time segment.
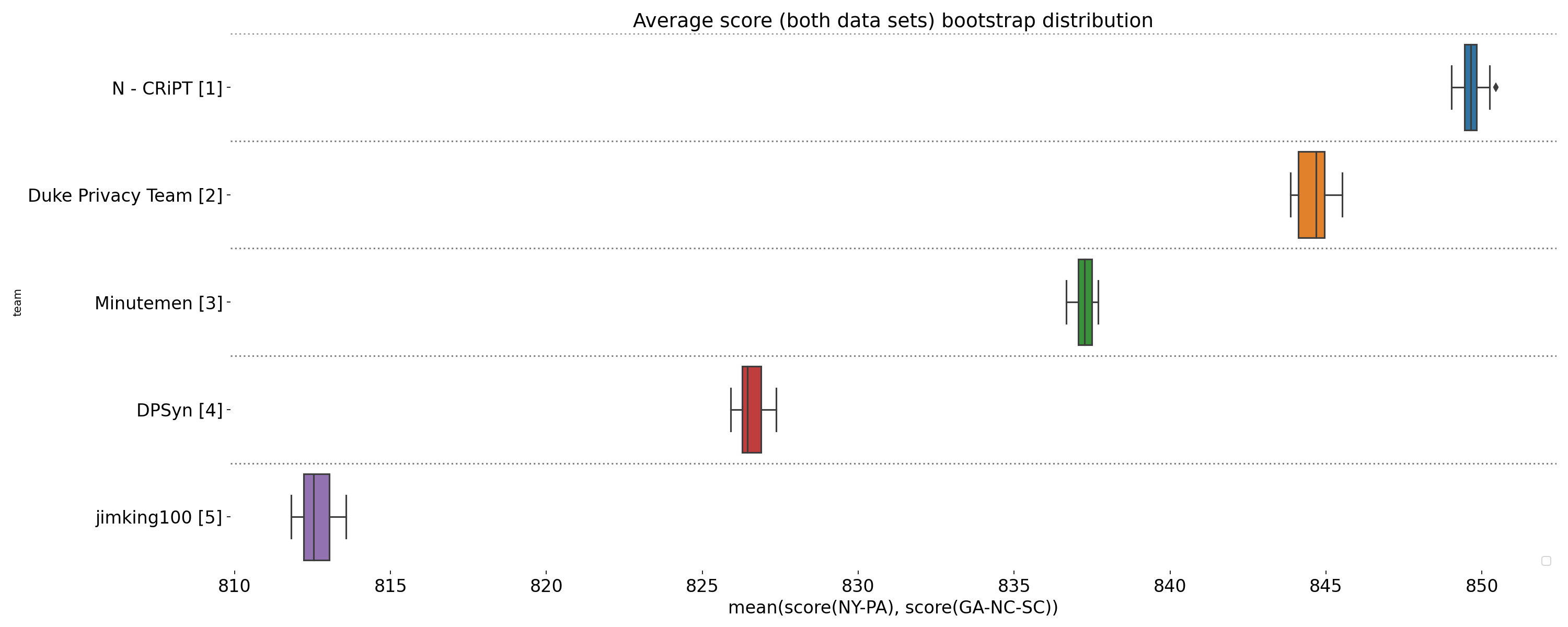
Visualization of boxplots showing the final score distribution for four runs on each sequestered data set (NY-PA and GA-NC-SC), displayed for teams whose solutions were validated as differentially private. Each run uses 3x as many k-marginal iterations as in the Development Phase.
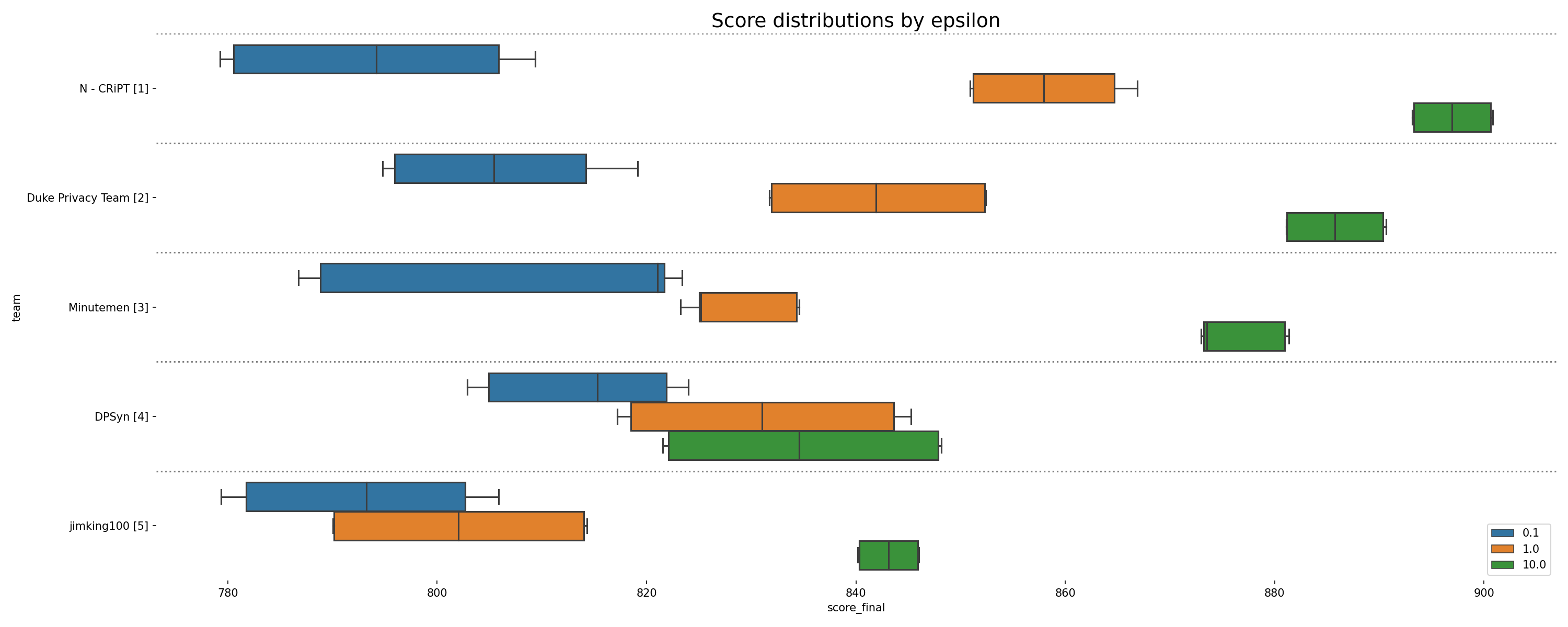
Scores grouped by epsilon (privacy parameter) for four separate runs on each final scoring dataset. The box represents the 25th, 50th (median), and 75th percentiles, while the whiskers represent 1.5 times the interquartile range.
In the end, 7 teams submitted to final scoring and 5 achieved submissions that were validated as differentially private. One result of the increased query sensitivity in the temporal map challenge is that it is important for solutions to interact with the data strategically, in order to get the most value from each query. Techniques that were able to make efficient use of their queries performed well, especially at higher epsilons. At the lowest epsilon (and highest privacy setting), all teams and all techniques performed poorly. This may reflect a fundamental limit in the privacy/accuracy trade-off for this problem.
Congratulations to all the participants in this sprint! Meet the winners below and check out their approaches to help public safety agencies share data while protecting privacy!
Participate in Sprint 3¶
Get in on the last sprint before it's too late! Submissions for Sprint 3 are now open, with a new $79,000 prize purse! You are welcome to join in Sprint 3 regardless of whether you participated in previous sprints.
This sprint includes data on taxi trips in the city of Chicago. Participants will have the chance to generate synthetic records of taxi trips that preserve undelying patterns in features, routes, and (for the first time this challenge!) the activity of individual taxis. Again, if you haven’t worked with synthetic data before, you might like to look through some of the solutions for the NIST 2018 Differential Privacy Synthetic Data Challenge (DeID1), which you can find here (scroll down to the Challenge section).
This is a fantastic finale to the DeID2 algorithm sprint series. We can't wait to see what you come up with.
Meet the winners: Sprint 2¶
N - CRiPT¶
Place: 1st
Prize: $15,000
Team members: Bolin Ding, Xiaokui Xiao, Kuntai Cai, Ergute Bao, Jianxin Wei
Hometown: China
Affiliation: National University of Singapore; Alibaba Group
Background:
We are a group of researchers interested in differential privacy.
What motivated you to participate?:
To apply our research on differential privacy in a practical setting.
Summary of approach:
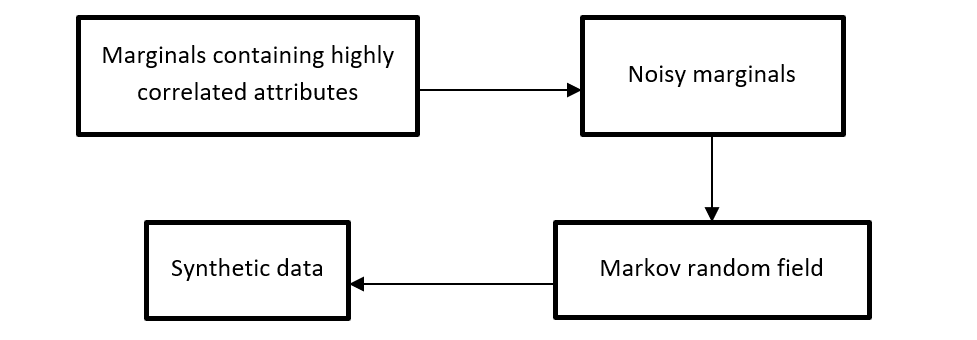
We used the public dataset to select a set of marginals that contain highly correlated attributes. Then, we inject noise to those marginal to achieve differential privacy, and used those marginals to construct a Markov random field (MRF). Finally, we use the MRF to generate synthetic data.
Duke DP Team¶

|

|
Place: 2nd
Prize: $10,000
Team members: Johes Bater, Yuchao Tao
Hometown: St. Louis, MO; Shanghai, China
Affiliation: Duke University
Background:
We are from the Duke privacy group and we study security and privacy.
What motivated you to participate?:
It’s challenging to see how privacy technologies can be applied to real problems.
Summary of approach:
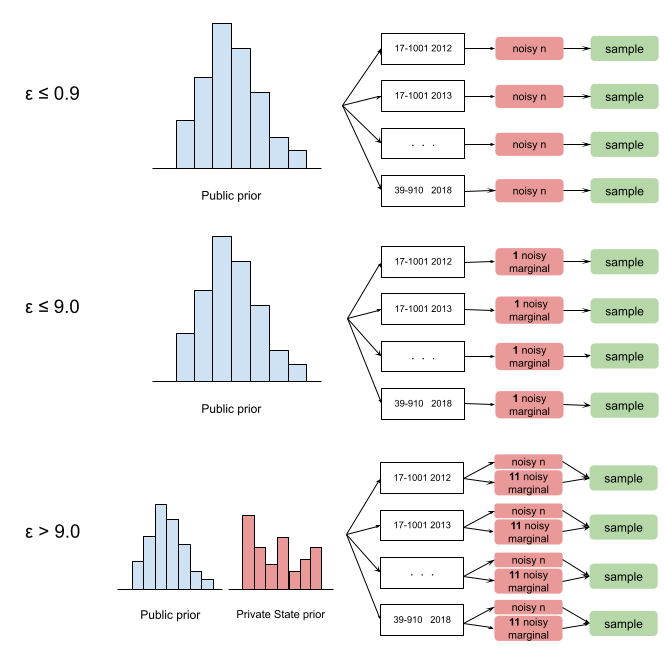
We apply an adaptive strategy for releasing the synthetic dataset for each puma-year group. When epsilon is high, we use 10 percent of the privacy budget to learn the selected high-way marginals over the entire state to adjust the prior distribution for each state, and then use the remaining 90 percent of the privacy budget to learn the selected one-way marginals to adjust the prior distribution for each puma-year. The marginals are selected based on maximum independence, maximum variation and minimum domain size principle. The prior update is related to the maximum entropy principle. When epsilon is low or moderate, we do less update to the prior.
Minutemen¶

|

|

|

|

|

|
Place: 3rd
Prize: $5,000
Team members: Ryan McKenna, Joie Wu, Arisa Tajima, Brett Mullins, Siddhant Pradhan, Cecilia Ferrando
Hometown: Cumberland, ME; Norristown, PA; Tokyo, Japan; Gainesville, GA; Mumbai, India; Torino, Italy
Affiliation: UMass Amherst
Background:
We are graduate students at UMass who do research on differential privacy.
What motivated you to participate?:
We are all differential privacy researchers and we found the temporal and geographical aspect of the challenge very interesting.
Summary of approach:
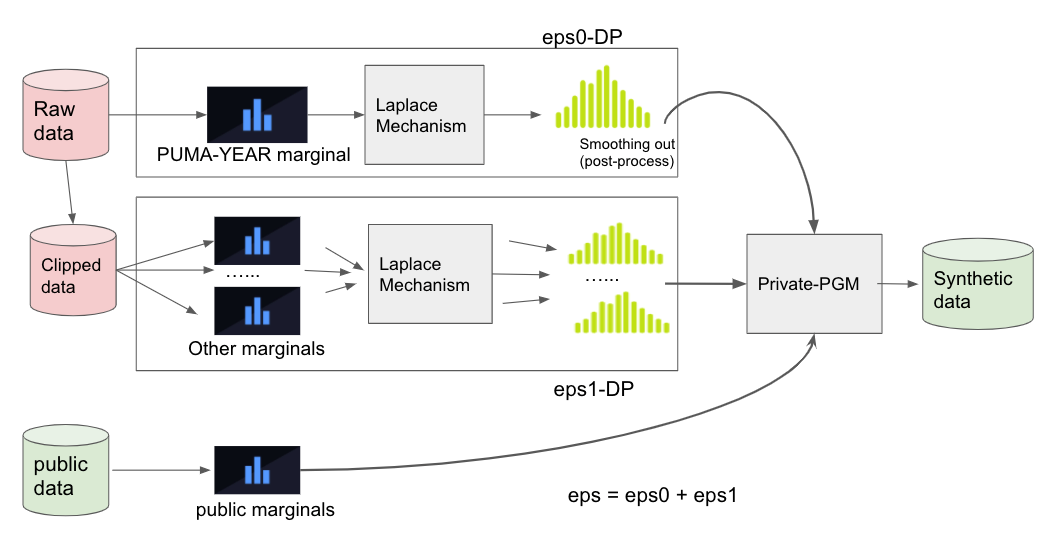
We used PGM inference to generate the synthetic data. Both noisy measurements and public measurements were used as an input for the Private-PGM which estimates graphical models to approximately match those marginals. Depending on epsilon, we carefully decided what pairs and how many pairs of marginals to measure privately and what attributes to measure from the public provisional dataset. To reduce sensitivity, we clipped the raw data where the number of clipped records were also decided based on the public data.
DPSyn¶
Place: 4th
Prize: $3,000
Team members: Ninghui Li, Zitao Li, Tianhao Wang
Hometown: West Lafayette, IN; China
Affiliation: Purdue University
Background:
We are a research group from Purdue University working on differential privacy. Our research group has been conducting research on data privacy for about 15 years, with a focus on differential privacy for the most recent decade. Our group has developed state-of-the-art algorithms for several tasks under the constraint of satisfying Differential Privacy and Local Differential Privacy.
What motivated you to participate?:
We have expertise in differential privacy. We also participated in earlier competitions held by NIST and got very positive results. We believe this is a good opportunity to think more about real world problems and explore the designs of algorithms.
Summary of approach:
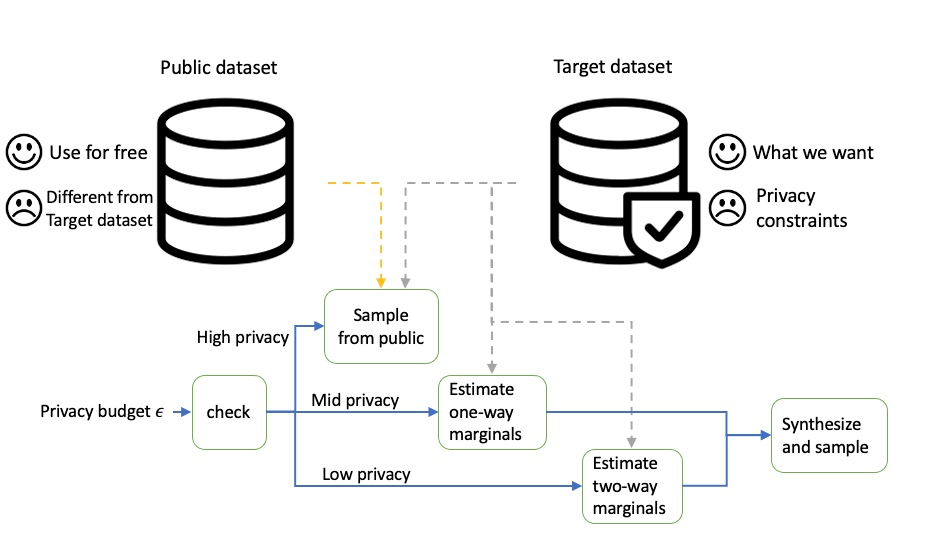
We consider the target dataset as a large dataset consisting of small sub-datasets with different PUMA-YEAR. In the strong privacy regime, we use all privacy budget to estimate the number of records for each sub-dataset and sample the estimated number of records from the public dataset. In the mid-privacy regime, we estimate all the one-way marginals for the target dataset in addition to the number of records for each sub-dataset, synthesize a large dataset, and sample from the synthetic data. We apply a similar strategy for the low privacy regime, except that we estimate two-way marginals instead of one-way marginals.
Jim King¶

|
Place: 5th
Prize: $2,000
Team members: Jim King
Hometown: Mill Valley, CA
Background:
I am a highly successful real estate agent who happens to like data science. My Computer Science degree, MBA in Finance and 20 years of experience in the tech field also help.
What motivated you to participate?:
I love learning, a challenge and competition! I was unaware of the differential privacy field prior to the contest so there was a steep learning curve with plenty of challenges. The competition and the chance to win cash was certainly a motivating factor.
Summary of approach:
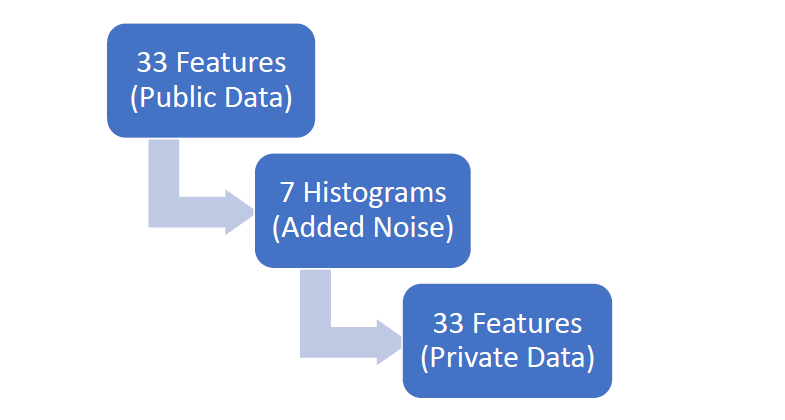
The algorithm calculates the number of simulated individuals for a single PUMA-year from the ground truth and noise is added using the Laplace mechanism to create the set of simulated individuals for each PUMA-year. In order to reduce the number of additional queries (to minimize added noise), the algorithm combines multiple related features and creates histograms (populations and weights) for each of the combined features, adding noise to each histogram using the Laplace mechanism. The 33 features are combined to create a total of 7 histograms. The simulated data is then created for each simulated user from the noisy histograms. For epsilons less than or equal to 1.0 all the public data is used and for epsilons greater than 1.0 data by PUMA is used.
Progressive Prizes¶
Finally, congratulations to DPSyn, Minutemen, Jim King, and N - CRiPT who each won a $1,000 progressive prize this sprint! As a reminder, progressive prizes are awarded part-way through each sprint to four eligible teams with the best scores to date, with precedence given to solutions that are pre-screened as satisfying differential privacy.
Don't forget, submissions are now open for Sprint 3. Head over to the competition for your chance to tackle a new problem and win $79,000 in prizes. Good luck!
Thanks to all the participants and to our winners! Special thanks to NIST PSCR for enabling this fascinating challenge!
*Banner image provided by Chicago Central Area Committee