blog

Cloudy with a chance of models


Huzzah. Our new competition predicting fog water collection from weather data is up! Let's put on our DATA SCIENCE HATS and get to work.

TL;DR version

Here's what we're doing right now: looking at the microclimate measurements as independent snapshots in time as predictors of the outcome variable. You can grab the notebook on Github and follow along at home.

Cool stuff we're not doing (but that the winners will undoubtedly explore)

Here's what we're NOT doing right now:

  • Using macro-climate weather data at different levels of sampling to add information and reduce variance.
  • Any form of time series modeling, like, at all.
  • Incorporating more complex models of the underlying system we wish to model. And by complex here we mean "vaguely realistic."

Here's a new term for y'all courtesy of the DrivenData team:

BM;IC Basic Model; Ignored Complexity

Somebody throw it on Urban Dictionary — let's make fetch happen. Okay, time to load up the tools of the trade.

In [1]:
%matplotlib inline
from __future__ import print_function

from matplotlib import pyplot as plt
import seaborn as sns

import numpy as np
import pandas as pd

Loading the data

For this benchmark, we are only going to use microclimate data.

In [2]:
microclimate_train = pd.read_csv('data/eaa4fe4a-b85f-4088-85ee-42cabad25c81.csv',
                                 index_col=0, parse_dates=[0])

microclimate_test = pd.read_csv('data/fb38df29-e4b7-4331-862c-869fac984cfa.csv',
                                index_col=0, parse_dates=[0])

labels = pd.read_csv('data/a0f785bc-e8c7-4253-8e8a-8a1cd0441f73.csv',
                     index_col=0, parse_dates=[0])

submission_format = pd.read_csv('data/submission_format.csv',
                                index_col=0, parse_dates=[0])

Looking at the training data (we are given labels for these)

First of all, let's just "walk around" this data a bit, and use the common summary functions to get a better idea for what it looks like.

In [3]:
microclimate_train.shape
Out[3]:
(5802, 9)
In [4]:
microclimate_train.describe()
Out[4]:
percip_mm humidity temp leafwet450_min leafwet460_min leafwet_lwscnt gusts_ms wind_dir wind_ms
count 5781.000000 5781.000000 5781.000000 5781.000000 4617.000000 5781.000000 5794.000000 5794.000000 5794.000000
mean 0.078972 0.554852 15.566805 0.991033 0.799972 457.476362 3.381701 135.184925 2.827167
std 0.973970 0.282715 7.126274 1.903983 1.743959 48.172783 1.832613 96.186550 1.637490
min 0.000000 0.000000 0.000000 0.000000 0.000000 297.625000 0.000000 0.000000 0.000000
25% 0.000000 0.319978 9.937500 0.000000 0.000000 438.583333 2.007544 60.760417 1.588485
50% 0.000000 0.496859 14.470833 0.000000 0.000000 441.625000 3.143336 102.041667 2.619792
75% 0.000000 0.827473 20.937500 0.000000 0.000000 447.000000 4.538977 209.656250 3.867351
max 24.250000 1.072792 36.508334 5.173913 5.000000 1023.000000 11.518700 355.000000 10.092204
In [31]:
microclimate_train.tail()
Out[31]:
percip_mm humidity temp leafwet450_min leafwet460_min leafwet_lwscnt gusts_ms wind_dir wind_ms
2015-12-22 14:00:00 0 0.342318 15.287500 0 0 439.041667 4.471919 78.458333 3.277452
2015-12-22 16:00:00 0 0.343302 14.754167 0 0 439.958333 3.109807 80.166667 2.099749
2015-12-22 18:00:00 0 0.351736 13.675000 0 0 440.916667 3.344510 71.375000 2.556580
2015-12-22 20:00:00 0 0.363110 12.862500 0 0 441.000000 4.375524 72.875000 3.973177
2015-12-22 22:00:00 0 0.377436 12.741667 0 0 441.000000 4.798827 65.333333 4.400671
In [6]:
microclimate_train.isnull().sum(axis=0)
Out[6]:
percip_mm           21
humidity            21
temp                21
leafwet450_min      21
leafwet460_min    1185
leafwet_lwscnt      21
gusts_ms             8
wind_dir             8
wind_ms              8
dtype: int64

Here's the big takeway: we will have to deal with some missing values.

Looking at the test data (we will be predicting labels for these rows)

In [7]:
microclimate_test.shape
Out[7]:
(1110, 9)
In [8]:
microclimate_test.describe()
Out[8]:
percip_mm humidity temp leafwet450_min leafwet460_min leafwet_lwscnt gusts_ms wind_dir wind_ms
count 1110.000000 1110.000000 1110.000000 1110.000000 918.000000 1110.000000 1110.000000 1110.000000 1110.000000
mean 0.015060 0.517156 15.563383 0.884949 0.527505 453.707082 3.348732 132.093260 2.805653
std 0.154859 0.265408 6.979713 1.816510 1.448019 35.884056 2.051050 94.138572 1.831789
min 0.000000 0.052849 2.237500 0.000000 0.000000 374.666667 0.000000 0.000000 0.000000
25% 0.000000 0.300331 10.662500 0.000000 0.000000 438.333333 1.857712 58.104167 1.433361
50% 0.000000 0.455093 14.272917 0.000000 0.000000 440.895833 2.902347 100.500000 2.405700
75% 0.000000 0.719250 20.813542 0.000000 0.000000 444.833333 4.625943 209.270833 3.971081
max 3.575000 1.037941 35.525000 5.041667 5.000000 690.833333 10.276614 349.666667 9.354568
In [10]:
microclimate_train.isnull().sum(axis=0)
Out[10]:
percip_mm           21
humidity            21
temp                21
leafwet450_min      21
leafwet460_min    1185
leafwet_lwscnt      21
gusts_ms             8
wind_dir             8
wind_ms              8
dtype: int64

So again, we will definitely need to pay attention to missing values and figure out smart ways to deal with that. File under #datascientistproblems.

Let's also plot all the data points in the training and test data to get a sense for how the data set is split:

In [11]:
fig, axs = plt.subplots(nrows=microclimate_train.shape[1], ncols=1, sharex=True, figsize=(16, 18))

columns = microclimate_train.columns
for i, ax in list(enumerate(axs)):
    col = columns[i]
    ax.plot_date(microclimate_train.index, microclimate_train[col], ms=1.5, label='train')
    ax.plot_date(microclimate_test.index, microclimate_test[col], ms=1.5, color='r', label='test')
    ax.set_ylabel(col)
    
    if i == 0:
        ax.legend(loc='upper right', markerscale=10, fontsize='xx-large')

This isn't your grandpa's random train/test split

Here's another fun insight: this problem has a time component and in the real world we are trying to predict the future. That is, we're trying to figure out the upcoming yield based on current weather. For those of us concerned about overfitting (hint: all of us), we will need to think hard about our modeling assumptions.

So, things that we could do but probably shouldn't:

  • Imputing missing values using all of the data.
  • Treating every data point as if it stands alone and is independent from other points in time.
  • Drawing on weather that hasn't happened yet to inform our current predictions.

But this is a benchmark and we're not all about rules on this blog. Watch us break every single one of these cautionary warnings below! (That's why they call it a benchmark. (Actually that statement doesn't make sense, we don't know why it's called a benchmark. (HOLY MOLY, TOO MANY PARENTHESES #inception #common-lisp)))

Looking at relationships between inputs and yield

In [12]:
print('train', microclimate_train.shape)
print('labels', labels.shape)

train (5802, 9)
labels (5802, 1)
In [13]:
microclimate_train.columns.tolist()
Out[13]:
['percip_mm',
 'humidity',
 'temp',
 'leafwet450_min',
 'leafwet460_min',
 'leafwet_lwscnt',
 'gusts_ms',
 'wind_dir',
 'wind_ms']
In [14]:
wanted_cols = [u'percip_mm', u'humidity', u'temp', u'leafwet450_min', u'leafwet_lwscnt', u'wind_ms']
wanted = microclimate_train[wanted_cols].copy().dropna()
wanted['yield'] = labels['yield']

sns.pairplot(wanted, diag_kind='kde')
plt.show()

We can see some relationships starting to emerge here, but maybe not as directly correlated with yield as we may have hoped.

Splitting the data

Quick nomenclature check: we are training our model on the competition's training data, but we still need to use some cross validation techniques to avoid overfitting the heck out of the data.

Spoiler alert: we still end up overfitting — you'll see! When you submit your killer AdaBoosted Neural TensorHustle&Flow, try not to do this. For bonus internet points on the forum, help our newer statistical modeling folks understand the limitations of this simple benchmark.

We'll go ahead and split up the competition training set into its own training and test sets for our modeling purposes here.

In [15]:
from sklearn.cross_validation import train_test_split

X_train, X_test, y_train, y_test = train_test_split(microclimate_train,
                                                    labels.values.ravel(),
                                                    test_size=0.3)

Building a model pipeline

Here's a scikit-learn pipeline which will handle a couple tasks for us in a well defined, repeatable way:

  • Setting up an imputer to replace missing data.
  • Try out some dimensionality reduction with PCA.
  • Train the world's most naive random forest classifier.

And we'll GRID SEARCH ALL THE THINGS, because, hey, why not, right???!1

Spoiler alert: there's a pretty good reason why this might not be a great idea. First one to point out why can be the provisional mayor of our forum with zero compensation but with no real responsibility.
In [16]:
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.preprocessing import Imputer
from sklearn.grid_search import GridSearchCV
from sklearn.ensemble import RandomForestRegressor

steps = [('imputer', Imputer()),
         ('pca', PCA()),
         ('rf', RandomForestRegressor())]
pipe = Pipeline(steps)

# create the grid search
params = {
    'pca__n_components': range(2, X_train.shape[1]),
    'imputer__strategy': ['mean', 'median', 'most_frequent'],
    'rf__n_estimators': [5, 10, 20]
}
estimator = GridSearchCV(pipe, param_grid=params, n_jobs=-1, verbose=1)
estimator.fit(X_train, y_train.ravel())

Fitting 3 folds for each of 63 candidates, totalling 189 fits

[Parallel(n_jobs=-1)]: Done  40 tasks      | elapsed:    5.5s
[Parallel(n_jobs=-1)]: Done 189 out of 189 | elapsed:   14.5s finished
Out[16]:
GridSearchCV(cv=None, error_score='raise',
       estimator=Pipeline(steps=[(u'imputer', Imputer(axis=0, copy=True, missing_values='NaN', strategy='mean', verbose=0)), (u'pca', PCA(copy=True, n_components=None, whiten=False)), (u'rf', RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
           max_features='auto', max_leaf_nod...imators=10, n_jobs=1, oob_score=False, random_state=None,
           verbose=0, warm_start=False))]),
       fit_params={}, iid=True, n_jobs=-1,
       param_grid={u'imputer__strategy': [u'mean', u'median', u'most_frequent'], u'pca__n_components': [2, 3, 4, 5, 6, 7, 8], u'rf__n_estimators': [5, 10, 20]},
       pre_dispatch='2*n_jobs', refit=True, scoring=None, verbose=1)
In [17]:
estimator.best_params_
Out[17]:
{u'imputer__strategy': u'most_frequent',
 u'pca__n_components': 8,
 u'rf__n_estimators': 20}

Examine performance

The competition uses root mean squared error as the metric, so let's see how we do on that front.

In [18]:
from sklearn.metrics import mean_squared_error

y_hat = estimator.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test, y_hat))
rmse
Out[18]:
1.9677692739292574

We can also plot our actuals against our predicted values and see if there's a trend.

In [38]:
fig, ax = plt.subplots(figsize=(8, 8))
plt.scatter(y_test, y_hat)

plt.xlabel('actual', fontsize=20)
plt.ylabel('predicted', fontsize=20)
plt.plot(np.linspace(0, 35), np.linspace(0, 35), label="$y=x$")

plt.xlim(0, 35)
plt.ylim(0, 35)
plt.legend(loc='upper left', fontsize=20)
plt.show()

Let's look at the residuals by themselves:

In [20]:
fig, ax = plt.subplots(figsize=(16, 4))
err = y_test - y_hat

ax.plot_date(X_test.index, err, c='r', ms=3)
ax.set_title('residuals on test data (each)', fontsize=20)
ax.set_ylabel('error')

plt.show()

And also look at the distribution of residuals.

In [21]:
fig, ax = plt.subplots(figsize=(16, 4))
plt.hist(err, bins=20, normed=True)
plt.title('residuals on test data (distribution)', fontsize=20)
plt.xlim(-20, 20)
plt.show()

So we have our predictions in hand, and we have some idea of the error (although in practice this number only makes sense compared to other submissions — yet another great reason to give people a benchmark even with a very naive model!)

Time to make this into a submission.

What should our submission look like?

So we know we need to predict the labels from the training inputs we were given, but let's just double check how it's supposed to look.

In [22]:
!head data/submission_format.csv

,yield
2013-11-24 00:00:00,0.0
2013-11-24 02:00:00,0.0
2013-11-24 04:00:00,0.0
2013-11-24 06:00:00,0.0
2013-11-24 08:00:00,0.0
2013-11-24 10:00:00,0.0
2013-11-24 12:00:00,0.0
2013-11-24 14:00:00,0.0
2013-11-24 16:00:00,0.0
In [23]:
submission_format.head()
Out[23]:
yield
2013-11-24 00:00:00 0
2013-11-24 02:00:00 0
2013-11-24 04:00:00 0
2013-11-24 06:00:00 0
2013-11-24 08:00:00 0
In [24]:
submission_format.dtypes
Out[24]:
yield    float64
dtype: object
Careful. There is a gotcha lurking here, which is that we are only using microclimate data in this benchmark and ignoring the other available data—but the microclimate test data has some missing values! How you deal with these is up to you (see above), but make sure you make predictions for every row expected in the submission format.
In [25]:
submission_format.shape
Out[25]:
(1590, 1)
In [26]:
microclimate_test.shape
Out[26]:
(1110, 9)

We'll do a quick and dirty mitigation by making sure the test data we pass into our pipline has an input row for each and every expected row in the submission format, even if they are all NaNs.

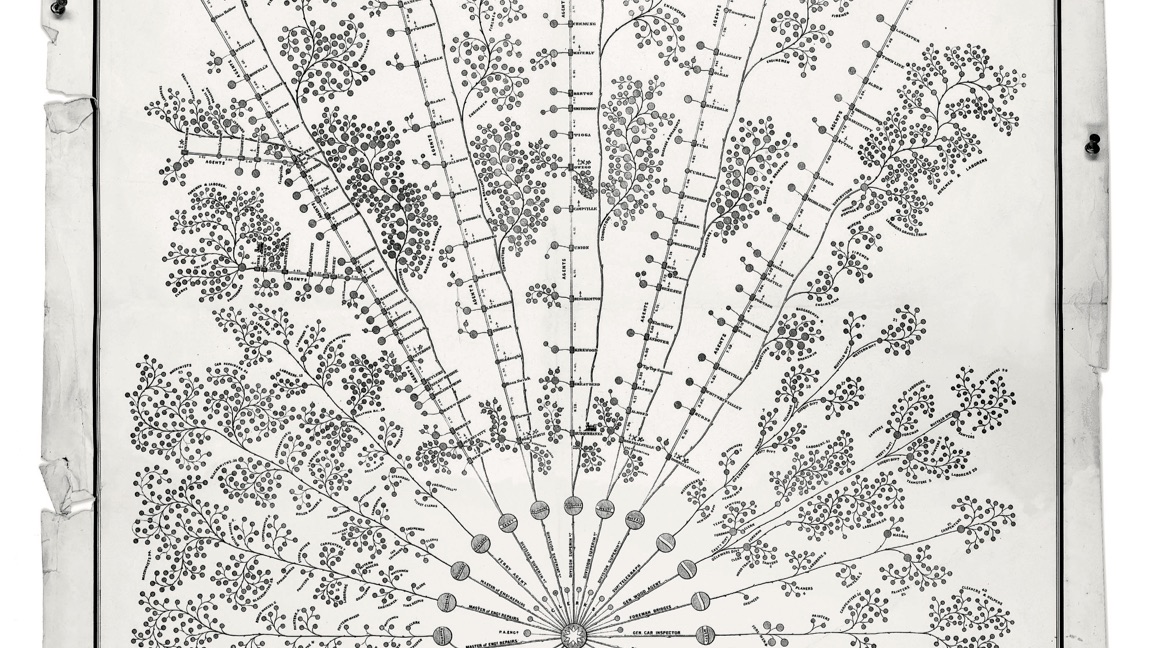
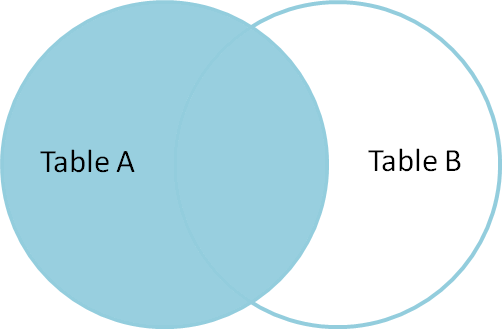
An easy way to get the right index for our purposes is a left outer join, where the "left hand" table is our submission format and the "right hand table" is the microclimate data we have. The left join will link every row that has an identical index in both sets, but will fill the rows in microclimate that do not exist as NaNs.

Here's a helpful figure from Jeff Atwood's helpful post on the topic:

In [27]:
test = submission_format.join(microclimate_test, how='left')  # left join onto the format
test = test[microclimate_test.columns]  # now just subset back down to the input columns

assert (test.index == submission_format.index).all()

Making our submission

We'll make predictions and fill in the yield column with actual outputs from our model:

In [28]:
submission_format['yield'] = estimator.predict(test)

Now we'll write it out to a file:

In [29]:
submission_format.to_csv("first_submission.csv")

And we can submit it to the competition and see what we end up with:

Ouch. The overfitting police have come to lay down the law. Note how we ended up scoring much more poorly on the withheld evaluation data than on our own withheld test set. That's a clear indication we overfit the data.

But the gauntlet has been thrown down. Will you step up to beat this ... pettifogging model?