Your first thought may be that penguins are charming, or adorable, or loving, or inspiring. And, you're not wrong. But, more importantly, penguins are indicators for the health of the Antarctic ecosystem. Penguin populations are affected by the complex dynamics between krill, fish, sea ice, predators, weather patterns, and the changing climate. Monitoring these populations can provide insight to the changes both natural and anthopogenic that are effecting earth's ecologies.
In our new competition, we're helping to make it easier for research teams to monitor penguin populations by predicting population estimates for three different species of penguins in sites throughout Antarctica.
In this post, we'll walk through a very simple first pass model, showing you how to load the data, make some predictions, and then submit those predictions to the competition.
Okay, to get things rolling, let's load up the basic tools of the trade:
%matplotlib inline
from __future__ import print_function
from __future__ import division
import os
import pandas as pd
import numpy as np
from tqdm import tqdm_notebook
from matplotlib import pyplot as plt
from matplotlib.colors import rgb2hex
import seaborn as sns
import statsmodels.api as sm
# let's not pollute this blog post with warnings
from warnings import filterwarnings
filterwarnings("ignore")
Loading the data¶
On the data download page, we provide a couple of datasets to get started:
All penguin observations: these are penguin counts for sites throughout the Antarctic. This is our main dataset, and all of these observations are compiled from published scientific literature. It contains information about the site, the kind of penguin, when the observation was, and how many penguins were counted. Additionally, it includes a measure of the error in the penguin count.
Nest count timeseries: Nests are one of the most reliable ways to estimate penguin populations. Usually there is one nest per breeding pair, and the nests--unlike the penguins--mostly stay in the same place. In this competition, we'll be predicting the nest counts in the seasons after 2013. This dataset has all of the nest counts from the entire set of observations laid out as a timeseries.
Nest error timeseries: We've also included the estimated error in the count as a timeseries. We'll use this when calculating how effective our predictions are.
One of the things we're most excited about is that this is an open data challenge. You can use any public data you can get your hands on to make predictions--as long as that data is not counts of penguins! We won't explore any of the other potential covariates here, but we encourage you to explore the literature and to experiment.
observations = pd.read_csv(
os.path.join("data", "training_set_observations.csv"), index_col=0
)
observations.head()
print(
"We have {} penguin observations from {} to {} at {} unique sites in the Antarctic!".format(
observations.shape[0],
observations.season_starting.min(),
observations.season_starting.max(),
observations.site_id.nunique(),
)
)

So let's take a look at what is in the data, and see the species, where they live, and how we've estimated their populations. First, we see that there are three species in this dataset. The MAPPPD project also collects data for emporer penguins--the stars of March of the Penguins--but their populations are different from these three species, so they are not included for this competition.
# How many observations do we have for each species?
observations.common_name.value_counts()
# How many differnet sites do we see each species at?
(observations.groupby("common_name").site_id.nunique())
# How many count types do we have for each species?
(observations.groupby("common_name").count_type.value_counts())
The counts for chicks and adults could possibly be useful as features, but in this benchmark we'll just be using the nest counts. We'll leave it up to you to experiment with integrating the other counts in your models.
Since we have locations for our data, it's sometimes helpful to see where they are on a map. We won't incorporate this spatial information into our benchmark, but we suspect it will be useful to competitors.
import folium
# Give each species a color
penguin_colors = {
"adelie penguin": rgb2hex(plt.get_cmap("Set1").colors[0]),
"chinstrap penguin": rgb2hex(plt.get_cmap("Set1").colors[2]),
"gentoo penguin": rgb2hex(plt.get_cmap("Set1").colors[3]),
}
# Setup a map of Antarctica
ice_map = folium.Map(
location=[-69.1759, -11.6016], tiles="Mapbox Bright", zoom_start=2, min_zoom=1
)
# Add 500 observations to the map
for i, row in observations.sample(500).iterrows():
(
folium.CircleMarker(
location=[row.latitude_epsg_4326, row.longitude_epsg_4326],
radius=3 + np.sqrt(row.penguin_count) / 40,
color=penguin_colors[row.common_name],
fill_color=penguin_colors[row.common_name],
).add_to(ice_map)
)
# Display the map
ice_map
Now that we've looked at all of our observations, let's turn to the prediction task for this competition--nest counts. The first thing we'll do is load the nest_count data. Note that a combination of a site_id and a common_name specify a particular timeseries, so we use the index_col=[0, 1] parameter in pandas to use both those columns in our index.
nest_counts = pd.read_csv(
os.path.join("data", "training_set_nest_counts.csv"), index_col=[0, 1]
)
# Let's look at the first 10 rows, and the last 10 columns
nest_counts.iloc[:10, -10:]
Now that we have loaded the nest counts, we will get a sense for what the data in the matrix looks like. We already see a lot of NaNs above, so we will plot a heatmap to see where we are missing data.
# get a sort order for the sites with the most observations
sorted_idx = pd.notnull(nest_counts).sum(axis=1).sort_values(ascending=False).index
# get the top 25 most common sites and divide by the per-series mean
to_plot = nest_counts.loc[sorted_idx].head(25)
to_plot = to_plot.divide(to_plot.mean(axis=1), axis=0)
# plot the data
plt.gca().matshow(to_plot, cmap="viridis")
plt.show()
Handle Missing Data¶
We can see that there is are many gaps in observations. Most time series models don't work well with missing data, so we'll have to think about clever ways to deal with this.
For this benchmark, we're just going to keep it simple and forward fill the counts from the last recorded observation. We also don't really start to see frequent observations until after 1980, so we're going to ignore data from before that just to keep things simple.
These assumptions about filling modeling missing data is one of the most important questions in this competition. We're taking a very simple approach, but some additional sophistication in your model will improve your score drastically.
def preprocess_timeseries(timeseries, first_year, fillna_value=0):
"""Takes one of the timeseries dataframes, removes
columns before `first_year`, and fills NaN values
with the preceeding value. Then backfills any
remaining NaNs.
As a courtesy, also turns year column name into
integers for easy comparisons.
"""
# column type
timeseries.columns = timeseries.columns.astype(int)
# subset to just data after first_year
timeseries = timeseries.loc[:, timeseries.columns >= first_year]
# Forward fill count values. This is a strong assumption.
timeseries.fillna(method="ffill", axis=1, inplace=True)
timeseries.fillna(method="bfill", axis=1, inplace=True)
# For sites with no observations, fill with fill_na_value
timeseries.fillna(fillna_value, inplace=True)
return timeseries
nest_counts = preprocess_timeseries(nest_counts, 1980, fillna_value=0.0)
nest_counts.head()
# get the top 25 most common sites and divide by the per-series mean
to_plot = nest_counts.loc[sorted_idx].head(25)
to_plot = to_plot.divide(to_plot.mean(axis=1), axis=0)
plt.gca().matshow(to_plot, cmap="viridis")
plt.show()
The Error Metric - Adjusted MAPE¶
Performance is evaluated according to an adjusted MAPE calculation. Since some penguin counts have differing accuracies, the percent error is weighted differently based on this expected accuracy.
We provide e_n values for all of the data in the training set. Using this custom metric in your model cross-validation will help improve your score on the leaderboard. We'll load these per-observation error data and use that in our model fitting.
e_n_values = pd.read_csv(os.path.join("data", "training_set_e_n.csv"), index_col=[0, 1])
# Process error data to match our nest_counts data
e_n_values = preprocess_timeseries(e_n_values, 1980, fillna_value=0.05)
e_n_values.head()
def amape(y_true, y_pred, accuracies):
"""Adjusted MAPE"""
not_nan_mask = ~np.isnan(y_true)
# calculate absolute error
abs_error = np.abs(y_true[not_nan_mask] - y_pred[not_nan_mask])
# calculate the percent error (replacing 0 with 1
# in order to avoid divide-by-zero errors).
pct_error = abs_error / np.maximum(1, y_true[not_nan_mask])
# adjust error by count accuracies
adj_error = pct_error / accuracies[not_nan_mask]
# return the mean as a percentage
return np.mean(adj_error)
# Let's confirm the best possible score is 0!
amape(nest_counts.values, nest_counts.values, e_n_values.values)
Building a Model¶

There are many, many ways to think about building forecasts for these penguin populations. The most accurate ones will probably use outside data as covariates in modeling the penguin populations. Here, we'll stick to a simple model.
We'll make the assumption that there is a linear trend to the population at each site separate site. We'll also make the assumption that there are some outliers in the historical data, so we want to only use a limited number of points to fit the model.
For every site in the dataset, we'll test fitting a model with the following procedure:
- Create a train/test split like the one in the competition (4 years).
- Test a linear model using only the most recent
Xpoints, where we varyXfrom 2 up to all of the data. - Predict with those models and see which value of
Xdoes the best on the future data. - Retrain the model on the entire dataset (through 2013) using that value of
X. - Store that model and
Xfor that site.
from sklearn.linear_model import LinearRegression
def train_model_per_row(ts, acc, split_year=2010):
# Split into train/test to tune our parameter
train = ts.iloc[ts.index < split_year]
test = ts.iloc[ts.index >= split_year]
test_acc = acc.iloc[acc.index >= split_year]
# Store best lag parameter
best_mape = np.inf
best_lag = None
# Test linear regression models with the most recent
# 2 points through using all of the points
for lag in range(2, train.shape[0]):
# fit the model
temp_model = LinearRegression()
temp_model.fit(train.index[-lag:].values.reshape(-1, 1), train[-lag:])
# make our predictions on the test set
preds = temp_model.predict(test.index.values.reshape(-1, 1))
# calculate the score using the custom metric
mape = amape(test.values, preds, test_acc.values)
# if it's the best score yet, hold on to the parameter
if mape < best_mape:
best_mape = mape
best_lag = lag
# return model re-trained on entire dataset
final_model = LinearRegression()
final_model.fit(ts.index[-best_lag:].values.reshape(-1, 1), ts[-best_lag:])
return final_model
Great, our training function is prepped and ready to go. Now, let's train our models!
models = {}
for i, row in tqdm_notebook(nest_counts.iterrows(), total=nest_counts.shape[0]):
acc = e_n_values.loc[i]
models[i] = train_model_per_row(row, acc)
At this point, we've trained a model for every site/species combination in the dataset, so all we need to do is make our predictions for 2014-2017. We'll load the submission format so that we can use that for structuring our predictions.
submission_format = pd.read_csv(
os.path.join("data", "submission_format.csv"), index_col=[0, 1]
)
print(submission_format.shape)
submission_format.head()
And now to make our predictions! We will go through every row in the submission file. For that site_id + common_name, we'll grab our trained model and lag. We'll then use that model to predict into the future!
preds = []
# For every row in the submission file
for i, row in tqdm_notebook(
submission_format.iterrows(), total=submission_format.shape[0]
):
# get the model for this site + common_name
model = models[i]
# make predictions using the model
row_predictions = model.predict(submission_format.columns.values.reshape(-1, 1))
# keep our predictions, rounded to nearest whole number
preds.append(np.round(row_predictions))
# Create a dataframe that we can write out to a CSV
prediction_df = pd.DataFrame(
preds, index=submission_format.index, columns=submission_format.columns
)
prediction_df.head()
Time to make a submission¶
All we have to do now is save our predictions and make a submission. Just to confirm that we're following the submission format, let's look at the first few rows:
prediction_df.to_csv("predictions.csv")
!head -n 5 predictions.csv
Looks good, now we can submit it to the competition.
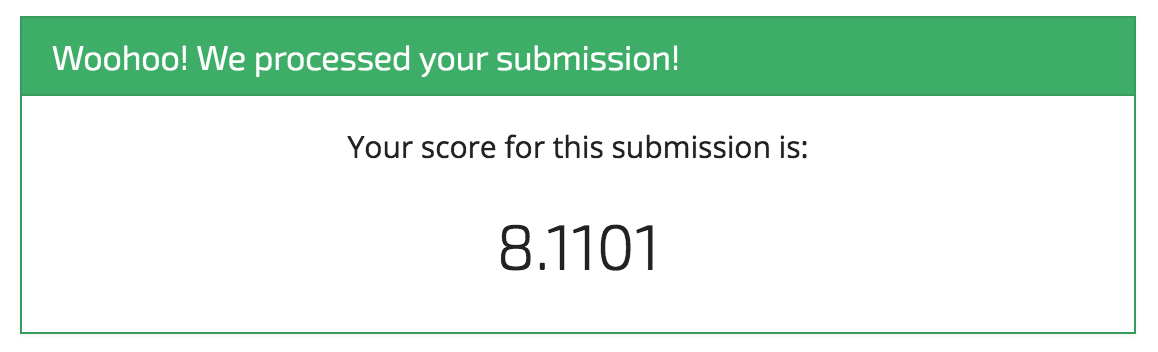
Woohoo! It's a start! And that's exactly what we intend with these benchmarks.
We're sure you'll be able to top this model in no time, and we can't wait to see what you come up with.