Optimizing Demand-side Strategies¶
Background¶
Flexibility can be defined as "the ability of a resource, whether any component or collection of components of the power system, to respond to the known and unknown changes of power system conditions at various operational timescales". The exploitation of flexibility is essential to avoid costly reinforcements of the power system and maintain security of supply while increasing the penetration of renewable (and intermittent) sources of energy.
Flexibility can be produced in different manners. It might come from generation options, from energy storage or from energy demand. In some cases, generation can also be proposed through alternative dispatchable assets such as Combined Heat and Power (CHP). Storage is valid for both electricity and heat. Energy storage is an easy way to increase building flexibility, provided there is a business case for such an investment. The present challenge is focused on making a good usage of an installed storage system.
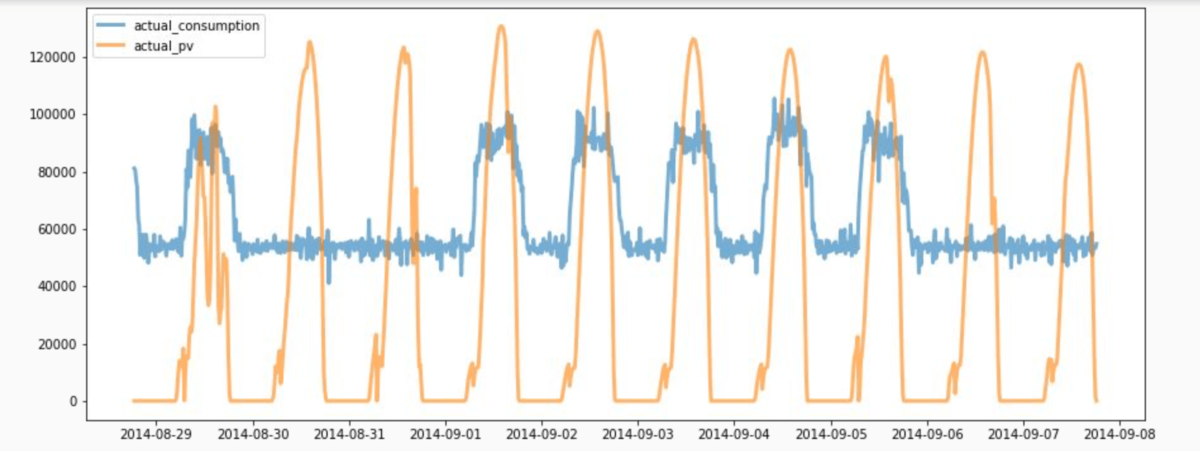
Viewed from the demand side, as in the case of smart buildings, time-of-use tariffs incentivize consumers to use energy when it is cheapest (and most abundant). Given such a tariff, the goal is to buy more energy when its price is the lowest, and buy less (or possibly sell) energy when its price is the highest.
The goal in this competition is to build an algorithm that controls a battery charging system and spends the least amount of money over a simulation period.
** In this competition data scientists all over the world built algorithms that control a battery charging system and spend the least amount of money over a simulation period. **
The competitors used traditional optimization tools like Linear Programs and constrained optimization, but also leverged machine learning and measurements of uncertainty to build the most reliable optimization sustem.

Meet the winners below!
Meet the winners¶
Team VietNam national ORlab¶

|

|

|

|

|
Place: 1st
Prize: €12,000
Hometowns: Vietnam
Username: ORLab, duymanhit: Minh Hoàng Hà, Duy Mạnh Vũ, Thị Thanh Lâm Vũ, Văn Phú Hoàng, Tiến Thành Đàm
Background:
- Minh Hoàng Hà is currently a lecturer at University of Engineering and Technology, Vietnam National University. His research interests include combinatorial optimization problems such as packing, scheduling and routing.
- Duy Mạnh Vũ is currently a second-year undergraduate student at University of Engineering and Technology, Vietnam National University. He likes studying operations research and machine learning.
- Thị Thanh Lâm Vũ is studying Computer Science at University of Engineering and Technology, Vietnam National University as a second-year undergraduate student. Her main interests are optimization methods applied in transportation and electric production.
- Văn Phú Hoàng is a second-year undergraduate student at University of Engineering and Technology, Vietnam National University. His plan in the near future is working on data mining and optimization.
- Tiến Thành Đàm is an undergraduate student at University of Engineering and Technology, Vietnam National University. He decided to follow optimization and data mining after working on the project "Power Laws: Optimizing Demand-side Strategies" of ORLab organized by DrivenData.
Summary of approach:
We considered the problem as a dynamic optimization problem. The problem at each step was modeled as a linear programming (LP). We selected Ortools to solve LP model optimally because it seemed to be the fastest and easy to install on the docker.
The next idea comes from the fact that in some cases where the coming s are enough to fully charge the battery, the solution provided by Ortools suggests us to charge a quantity of energy that is higher than the real difference of production and consummation. And as a result, we have to buy electric from the grid to supplement the variance in the forecast. We then tried to adjust the solution obtained from Ortools to take into account the uncertainty of the forecast such that the value of the new solution objective function is kept the same. To do so, from the obtained solution, we will find a period p (normally in daytime) in which the battery is consecutively not discharged and (pv_i – load_i ≥ 0) for each step i in p. We then try to charge a quantity of (pv_i – load_i – reducedEnergy) for each step during the period. Here, pv_i and load_i are the forecasting amount of production of PV and consummation of building at step i respectively; reducedEnergy is a fixed amount of energy that is reduced equally in all steps of the period p. We will find the maximal value of reducedEnergy so that the total quantity of charged energy in the considering period is kept the same as in the optimal solution provided by Ortools and the power limit constraint is still satisfied. Note that, the larger the value of reducedEnergy is, the more the risk of buying energy from grid decreases. The binary search is used to compute reducedEnergy. The similar idea is applied for the period where the battery is consecutively not charged and (pv_i – load_i ≤ 0) for each step i in the period.
Check out orlab’s full write-up and solution in the competition repo.
Guilllermo Barbadillo¶

Place: 2nd
Prize: €7,000
Hometown: Pamplona, Spain
Username: ironbar
Background: I am self-taught and I have learned artificial intelligence on my own. I have been participating in data science challenge for two years and this is my second prize. My long term goal (like Deepmind) is to solve intelligence. It was a very interesting challenge and the only thing that I regret is that I didn't have time to try on the other challenges, because they also seemed quite interesting.
Summary of approach:
My solution is based on simplificatoin of the period, dynamic programming, and intelligent pruning of the actions. A complete account of the approach is available in a presentation about the methods in the competition repo.
Check out ironbar's full write-up and solution in the competition repo.
Team Helios¶

|

|
Place: 3rd
Prize: €4,000
Hometown: Hanoi, Vietnam
Username: Team Helios: Hoa Nguyen Phuong (hoa.nguyen) and Huyen Tran Ngoc Nhat (XuHelios)
Background:
Hoa Nguyen Phuong received her B.Sc. degree from FPT University in Vietnam with the major on Computer Science in 2017. She is going to start her master program on Computer Science this September.
Huyen Tran Ngoc Nhat has recently graduated from FPT University in Vietnam. She now focuses on applying machine learning techniques to solve real-life problems.
Summary of approach:
Formulate a linear programming model for the optimization problem at each step with forecast data and use an open-source tool, which can be installed by pip to solve it. Scatter the energy charged (or discharged) among steps to avoid buying superfluous energy due to the uncertainty of next forecasts.
In the future, we should use cplex – the best lp/mip tool to improve the running time. From the historical data, we could find the probability distribution function for the variance in the forecast of pv and load; and then consider a robust optimization problem. More precisely, we would search for a solution such that the probability of buying additional energy from the grid due to uncertainty of the forecast is restricted to a given threshold.
Check out Helios's full write-up and solution in the competition repo.
Thanks to all the participants and to our winners! Special thanks to Schneider Electric for a fascinating challenge!