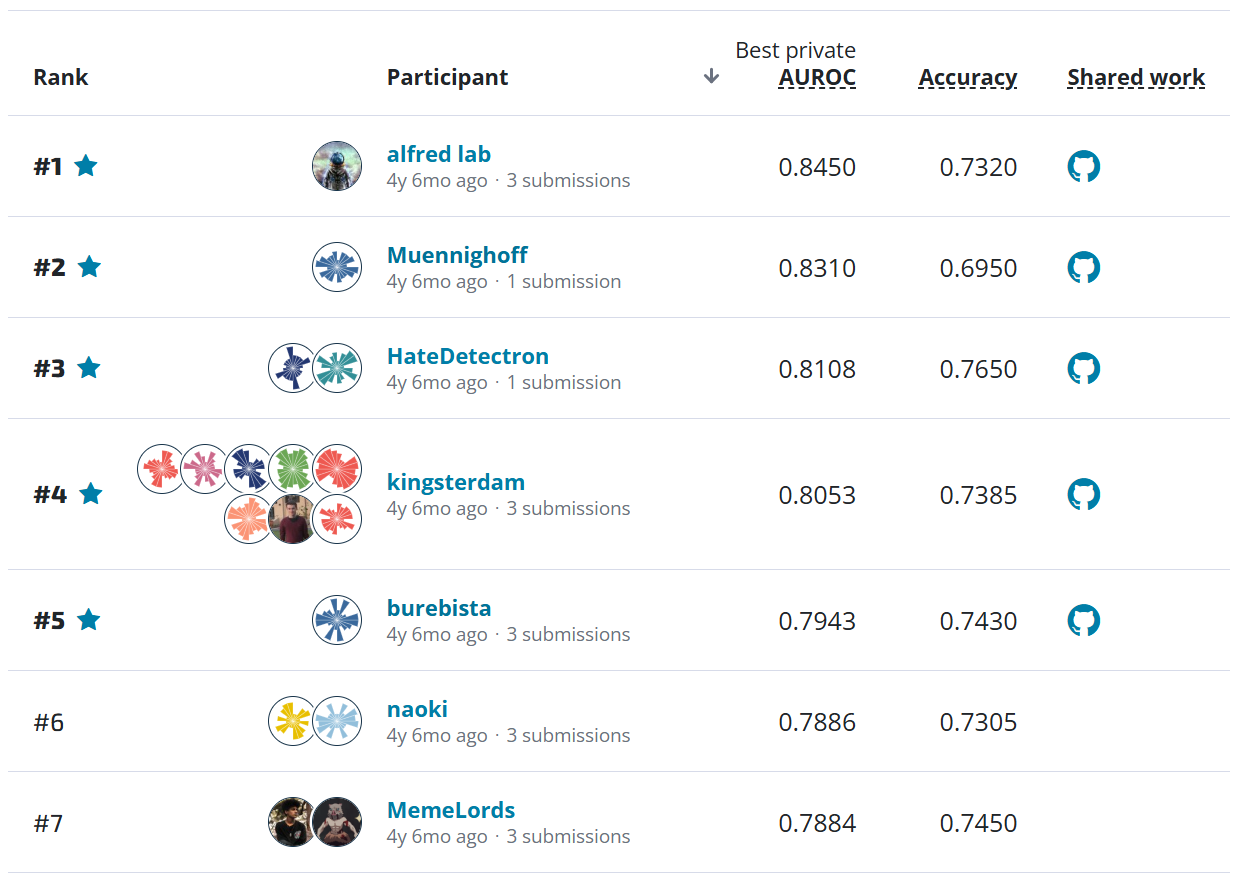
Pandemics have rarely taken center stage in the way they have this year with COVID-19. Vaccines are a key public health measure used to fight infectious diseases like COVID-19. They provide immunization for individuals, and enough immunization in a community can further reduce the spread of diseases through "herd immunity."
As of the writing of this post, vaccines for COVID-19 are still under development and not yet available. We will instead look at a recent historical pandemic, also of a highly infectious respiratory disease: the 2009 H1N1 influenza pandemic. The 2009 H1N1 flu virus, also called "swine flu," first appeared in the spring of 2009 and quickly spread across the world.
Vaccines for H1N1 were first publicly available in the United States in October 2009, when the United States government began a vaccination campaign. We will look at data from the National 2009 H1N1 Flu Survey collected to monitor vaccination rates during that campaign. This phone survey asked people whether they had received H1N1 and seasonal flu vaccines, in conjunction with information they shared about their lives, opinions, and behaviors. A better understanding of how these characteristics have been associated with personal vaccination patterns may provide guidance for future public health efforts.
In this post, we'll walk through the competition. We will show you how to load the data and do a quick exploratory analysis. Then, we will train a simple model, make some predictions, and then submit those predictions to the competition.
Loading the data¶
On the data download page, we provide everything you need to get started:
- Training Features: These are the input variables that your model will use to predict the probability that people received H1N1 flu and seasonal flu vaccines. There are 35 feature columns in total, each a response to a survey question. These questions cover several different topics, such as whether people observed safe behavioral practices, their opinions about the diseases and the vaccines, and their demographics. Check out the problem description page for more information.
- Training Labels: These are the labels corresponding to the observations in the training features. There are two target variables:
h1n1_vaccineandseasonal_vaccine. Both are binary variables, with 1 indicating that a person received the respective flu vaccine and 0 indicating that a person did not receive the respective flu vaccine. Note that this is what is known as a "multilabel" modeling task. - Test Features: These are the features for observations that you will use to generate the submission predictions after training a model. We don't give you the labels for these samples—it's up to you to generate them.
- Submission Format: This file serves as an example for how to format your submission. It contains the index and columns for our submission prediction. The two target variable columns are filled with 0.5 and 0.7 as an example. Your submission to the leaderboard must be in this exact format (with different prediction values) in order to be scored successfully!
Let's start by importing the libraries that we will need to load and explore the data.
from pathlib import Path
import numpy as np
import pandas as pd
pd.set_option("display.max_columns", 100)
Next, we can load the datasets and begin taking a look.
DATA_PATH = Path.cwd().parent / "data" / "final" / "public"
features_df = pd.read_csv(
DATA_PATH / "training_set_features.csv", index_col="respondent_id"
)
labels_df = pd.read_csv(DATA_PATH / "training_set_labels.csv", index_col="respondent_id")
print("features_df.shape", features_df.shape)
features_df.head()
Each row is a person who was a survey respondent. The columns are the feature values corresponding to those people. We have 26,707 observations and 35 features.
features_df.dtypes
Now let's look at the labels.
print("labels_df.shape", labels_df.shape)
labels_df.head()
We have the same 26,707 observations, and two target variables that we have labels for.
Let's double-check that the rows between the features and the labels match up. We don't want to have the wrong labels. Numpy's assert_array_equal will error if the two arrays—the row indices of the two data frames—don't match up.
np.testing.assert_array_equal(features_df.index.values, labels_df.index.values)
The assertion ran, and nothing happened. That's good, it means there is no problem. If the two index arrays were not the same, there would be an error.
Exploring the data¶
%matplotlib inline
import matplotlib.pyplot as plt
Labels¶
Let's start by taking a look at our distribution of the two target variables.
fig, ax = plt.subplots(2, 1, sharex=True)
n_obs = labels_df.shape[0]
(
labels_df["h1n1_vaccine"]
.value_counts()
.div(n_obs)
.plot.barh(title="Proportion of H1N1 Vaccine", ax=ax[0])
)
ax[0].set_ylabel("h1n1_vaccine")
(
labels_df["seasonal_vaccine"]
.value_counts()
.div(n_obs)
.plot.barh(title="Proportion of Seasonal Vaccine", ax=ax[1])
)
ax[1].set_ylabel("seasonal_vaccine")
fig.tight_layout()
It looks like roughy half of people received the seasonal flu vaccine, but only about 20% of people received the H1N1 flu vaccine. In terms of class balance, we say that the seasonal flu vaccine target has balanced classes, but the H1N1 flu vaccine target has moderately imbalanced classes.
Are the two target variables independent? Let's take a look.
pd.crosstab(
labels_df["h1n1_vaccine"], labels_df["seasonal_vaccine"], margins=True, normalize=True
)
# Phi Coefficient is the same as Pearson for two binary variables
(labels_df["h1n1_vaccine"].corr(labels_df["seasonal_vaccine"], method="pearson"))
These two variables have a phi coefficient of 0.37, indicating a moderate positive correlation. We can see that in the cross-tabulation as well. Most people who got an H1N1 flu vaccine also got the seasonal flu vaccine. While a minority of people who got the seasonal vaccine got the H1N1 vaccine, they got the H1N1 vaccine at a higher rate than those who did not get the seasonal vaccine.
Features¶
Next, let's take a look at our features. From the problem description page, we know that the feature variables are almost all categorical: a mix of binary, ordinal, and nominal features. Let's pick a few and see how the rates of vaccination may differ across the levels of the feature variables.
First, let's combine our features and labels into one dataframe.
joined_df = features_df.join(labels_df)
print(joined_df.shape)
joined_df.head()
Prototyping a Plot¶
Next, let's see how the features are correlated with the target variables. We'll start with trying to visualize if there is simple bivariate correlation. If a feature is correlated with the target, we'd expect there to be different patterns of vaccination as you vary the values of the feature.
Jumping right to the right final visualization is hard. We can instead pick one feature and one target and work our way up to a prototype, before applying it to more features and both targets. We'll use h1n1_concern, the level of concern the person showed about the H1N1 flu, and h1n1_vaccine as a target variable.
First, we'll get the count of observations for each combination of those two variables.
counts = (
joined_df[["h1n1_concern", "h1n1_vaccine"]]
.groupby(["h1n1_concern", "h1n1_vaccine"])
.size()
.unstack("h1n1_vaccine")
)
counts
It's hard to eyeball these raw numbers and see patterns clearly. Let's put this into a bar chart. We'll compare how the group sizes change as you vary h1n1_concern.
ax = counts.plot.barh()
ax.invert_yaxis()
ax.legend(loc="center right", bbox_to_anchor=(1.3, 0.5), title="h1n1_vaccine")
Unfortunately, it's still hard to tell whether h1n1_concern levels show differences in someone's likelihood to get vaccinated. Since the two classes are imbalanced, we just see fewer vaccinated observations for every level of h1n1_concern. It swamps out any other trends that might exist.
Let's instead look at the rate of vaccination for each level of h1n1_concern.
h1n1_concern_counts = counts.sum(axis="columns")
h1n1_concern_counts
props = counts.div(h1n1_concern_counts, axis="index")
props
ax = props.plot.barh()
ax.invert_yaxis()
ax.legend(loc="center left", bbox_to_anchor=(1.05, 0.5), title="h1n1_vaccine")
Now we have a clearer picture of what's happening! In this plot, each pair of blue (no vaccine) and orange (received vaccine) bars add up to 1.0. We can clearly see that even though most people don't get the H1N1 vaccine, they are more likely to if they have a higher level of concern. It looks like h1n1_concern will be a useful feature when we get to modeling.
Since every pair of bars adds up to 1.0 and we only have two bars, this is actually a good use case for a stacked bar chart, to make it even easier to read.
ax = props.plot.barh(stacked=True)
ax.invert_yaxis()
ax.legend(loc="center left", bbox_to_anchor=(1.05, 0.5), title="h1n1_vaccine")
This is a more compact plot showing the same thing as before.
Plotting more variables¶
Let's factor this code into a function so we can use it on more variables.
def vaccination_rate_plot(col, target, data, ax=None):
"""Stacked bar chart of vaccination rate for `target` against
`col`.
Args:
col (string): column name of feature variable
target (string): column name of target variable
data (pandas DataFrame): dataframe that contains columns
`col` and `target`
ax (matplotlib axes object, optional): matplotlib axes
object to attach plot to
"""
counts = joined_df[[target, col]].groupby([target, col]).size().unstack(target)
group_counts = counts.sum(axis="columns")
props = counts.div(group_counts, axis="index")
props.plot(kind="barh", stacked=True, ax=ax)
ax.invert_yaxis()
ax.legend().remove()
Then, we'll loop through several columns and plot against both h1n1_vaccine and seasonal_vaccine.
cols_to_plot = [
"h1n1_concern",
"h1n1_knowledge",
"opinion_h1n1_vacc_effective",
"opinion_h1n1_risk",
"opinion_h1n1_sick_from_vacc",
"opinion_seas_vacc_effective",
"opinion_seas_risk",
"opinion_seas_sick_from_vacc",
"sex",
"age_group",
"race",
]
fig, ax = plt.subplots(len(cols_to_plot), 2, figsize=(9, len(cols_to_plot) * 2.5))
for idx, col in enumerate(cols_to_plot):
vaccination_rate_plot(col, "h1n1_vaccine", joined_df, ax=ax[idx, 0])
vaccination_rate_plot(col, "seasonal_vaccine", joined_df, ax=ax[idx, 1])
ax[0, 0].legend(loc="lower center", bbox_to_anchor=(0.5, 1.05), title="h1n1_vaccine")
ax[0, 1].legend(loc="lower center", bbox_to_anchor=(0.5, 1.05), title="seasonal_vaccine")
fig.tight_layout()
It looks like the knowledge and opinion questions have pretty strong signal for both target variables.
The demographic features have stronger correlation with seasonal_vaccine, but much less so far h1n1_vaccine. In particular, we interestingly see a strong correlation with age_group with the seasonal_vaccine but not with h1n1_vaccine. It appears that with seasonal flu, people act appropriately according to the fact that people more impacted and have higher risk of flu-related complications with age. It turns out though that H1N1 flu has an interesting relationship with age: even though older people have higher risk of complications, they were less likely to get infected! While we know anything about causality from this analysis, it seems like the risk factors ended up being reflected in the vaccination rates.
Building some models¶
Let's start working on training some models! We will be using logistic regression, a simple and fast linear model for classification problems. Logistic regression is a great model choice for a first-pass baseline model when starting out on a problem.
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.multioutput import MultiOutputClassifier
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, roc_auc_score
RANDOM_SEED = 6 # Set a random seed for reproducibility!
We will be using scikit-learn's logistic regression implementation.
Standard logistic regression only works with numeric input for features. Since this is a benchmark, we're going to build simple models only using the numeric columns of our dataset.
Categorical variables with non-numeric values take a little more preprocessing to prepare for many machine learning algorithms. We're not going to deal with them in this benchmark walkthrough, but there are many different ways to encode categorical variables into numeric values. Check out one-hot encoding and ordinal encoding to get started if you're not familiar.
features_df.dtypes != "object"
numeric_cols = features_df.columns[features_df.dtypes != "object"].values
print(numeric_cols)
Feature Preprocessing¶
There are two important data preprocessing steps before jumping to the logistic regression:
- Scaling: Transform all features to be on the same scale. This matters when using regularization, which we will discuss in the next section. We will use
StandardScaler, also known as Z-score scaling. This scales and shifts features so that they have zero mean and unit variance. - NA Imputation: Logistic regression does not handle NA values. We will use median imputation, which fills missing values with the median from the training data, implemented with
SimpleImputer.
We are also going to start using Scikit-Learn's built-in composition functionality to encapsulate everything into a pipeline. Building pipelines is a best practice for building machine learning models. Among other benefits, it makes it easy to reuse on new data (such as our test data). The great thing about pipelines is that they have the same interface as transformers and estimators, so you can treat them as if they are.
In the block below, we're going to first chain together the preprocessing steps (scaling and imputing) into one intermediate pipeline object numeric_preprocessing_steps. Then, we use that with Scikit-Learn's ColumnTransformer, which is a convenient way to grab columns out of a pandas data frame and then apply a specified transformer.
If we wanted to do other transformations on other columns, such as encoding our non-numeric columns, that would be additional entries to the list in the transformers argument of ColumnTransformer.
# chain preprocessing into a Pipeline object
# each step is a tuple of (name you chose, sklearn transformer)
numeric_preprocessing_steps = Pipeline(
[
("standard_scaler", StandardScaler()),
("simple_imputer", SimpleImputer(strategy="median")),
]
)
# create the preprocessor stage of final pipeline
# each entry in the transformer list is a tuple of
# (name you choose, sklearn transformer, list of columns)
preprocessor = ColumnTransformer(
transformers=[("numeric", numeric_preprocessing_steps, numeric_cols)],
remainder="drop",
)
Next, we're going to define our estimators.
We'll use scikit-learn's default hyperparameters for LogisticRegression of L2 (a.k.a. Ridge) regularization with C value (inverse regularization strength) of 1. Regularization is useful because it reduces overfitting. Check out scikit-learn's documentation for LogisticRegression to read more about the options. When building your own model, you may want to tune your hyperparameters using something like GridSearchCV.
Because we have two labels we need to predict, we can use Scikit-Learn's MultiOutputClassifier. This is a convenient shortcut for training two of the same type of model and having them run together.
Estimator¶
estimators = MultiOutputClassifier(estimator=LogisticRegression(penalty="l2", C=1))
Putting Together the Full Pipeline¶
We put the preprocessing and the estimator stages together into one Pipeline object, which gives us one interface to run data through for everything.
full_pipeline = Pipeline(
[
("preprocessor", preprocessor),
("estimators", estimators),
]
)
We can see the full pipeline printed out below.
full_pipeline
Training and Evaluation¶
Finally, let's get ready to train and evaluate our model.
Let's split our available data into a training and evaluation set. (We're going to reserve "test set" to refer to the final predictions we upload to the platform.) We'll use a third of our data for evaluation.
Recall that earlier in our exploratory analysis, the h1n1_vaccine label classes were moderately imbalanced. Sometimes this can lead to lopsided splits, which can lead to generalization problems with fitting and/or evaluating the model. We should have a large enough dataset that a randomly shuffled split should keep the same proportions, but we can use the stratify argument to enforce even splits.
X_train, X_eval, y_train, y_eval = train_test_split(
features_df,
labels_df,
test_size=0.33,
shuffle=True,
stratify=labels_df,
random_state=RANDOM_SEED,
)
Now, let's train the model!
%%time
# Train model
full_pipeline.fit(X_train, y_train)
# Predict on evaluation set
# This competition wants probabilities, not labels
preds = full_pipeline.predict_proba(X_eval)
preds
print("test_probas[0].shape", preds[0].shape)
print("test_probas[1].shape", preds[1].shape)
This has given us back a list of two (n_obs, 2) arrays. The first array is for h1n1_vaccine, and the second array is for seasonal_vaccine. The two columns for each array are probabilities for class 0 and class 1 respectively. That means we want the second column (index 1) for each of the two arrays. Let's grab those and put them in a data frame.
y_preds = pd.DataFrame(
{
"h1n1_vaccine": preds[0][:, 1],
"seasonal_vaccine": preds[1][:, 1],
},
index=y_eval.index,
)
print("y_preds.shape:", y_preds.shape)
y_preds.head()
This competition uses ROC AUC as the metric. Let's plot ROC curves and take a look. Unfortunately, scikit-learn's convenient plot_roc_curve doesn't support multilabel, so we'll need to make the plot ourselves.
def plot_roc(y_true, y_score, label_name, ax):
fpr, tpr, thresholds = roc_curve(y_true, y_score)
ax.plot(fpr, tpr)
ax.plot([0, 1], [0, 1], color="grey", linestyle="--")
ax.set_ylabel("TPR")
ax.set_xlabel("FPR")
ax.set_title(f"{label_name}: AUC = {roc_auc_score(y_true, y_score):.4f}")
fig, ax = plt.subplots(1, 2, figsize=(7, 3.5))
plot_roc(y_eval["h1n1_vaccine"], y_preds["h1n1_vaccine"], "h1n1_vaccine", ax=ax[0])
plot_roc(
y_eval["seasonal_vaccine"], y_preds["seasonal_vaccine"], "seasonal_vaccine", ax=ax[1]
)
fig.tight_layout()
An AUC score of 0.5 is no better than random, and an AUC score of 1.0 is a perfect model. Both models look like they generally perform similarly. Our scores of around 0.83 are not great, but they're not bad either!
The competition metric is the average between these two AUC values. Scikit-learn's roc_auc_score does support multilabel, so we can use that directly.
roc_auc_score(y_eval, y_preds)
Retrain Model on Full Dataset¶
Now that we have an idea of our performance, we'll want to retrain our model on the full dataset before generating our predictions on the test set.
%%time
full_pipeline.fit(features_df, labels_df)
None # So we don't print out the whole pipeline representation
Generating the Predictions for the Test Set¶
Let's make predictions on the test set! Again, for this competition, we want the probabilities, not the binary label predictions. We'll again use the .predict_proba method to get those.
test_features_df = pd.read_csv(
DATA_PATH / "test_set_features.csv", index_col="respondent_id"
)
test_probas = full_pipeline.predict_proba(test_features_df)
test_probas
As before, this gives us back two arrays: one for h1n1_vaccine, and one for seasonal_vaccine. The two columns for each array are probabilities for class 0 and class 1 respectively. That means we want the second column (index 1) for each of the two arrays.
Let's read in the submission format file so we can put our predictions into it.
submission_df = pd.read_csv(
DATA_PATH / "submission_format.csv", index_col="respondent_id"
)
submission_df.head()
We want to replace those 0.5s and 0.7s with our predictions. First, make sure we have the rows in the same order by comparing the indices. Then, we can drop in the appropriate columns from our predicted probabilities.
# Make sure we have the rows in the same order
np.testing.assert_array_equal(test_features_df.index.values, submission_df.index.values)
# Save predictions to submission data frame
submission_df["h1n1_vaccine"] = test_probas[0][:, 1]
submission_df["seasonal_vaccine"] = test_probas[1][:, 1]
submission_df.head()
submission_df.to_csv("my_submission.csv", index=True)
!head my_submission.csv
Submit to the Leaderboard¶
We can then head over to the competition submissions page to submit the predictions.

Done!
Images courtesy of the
U.S. Navy
and the
Fort Meade Public Affairs Office
via Flickr under the
CC BY 2.0 license
.