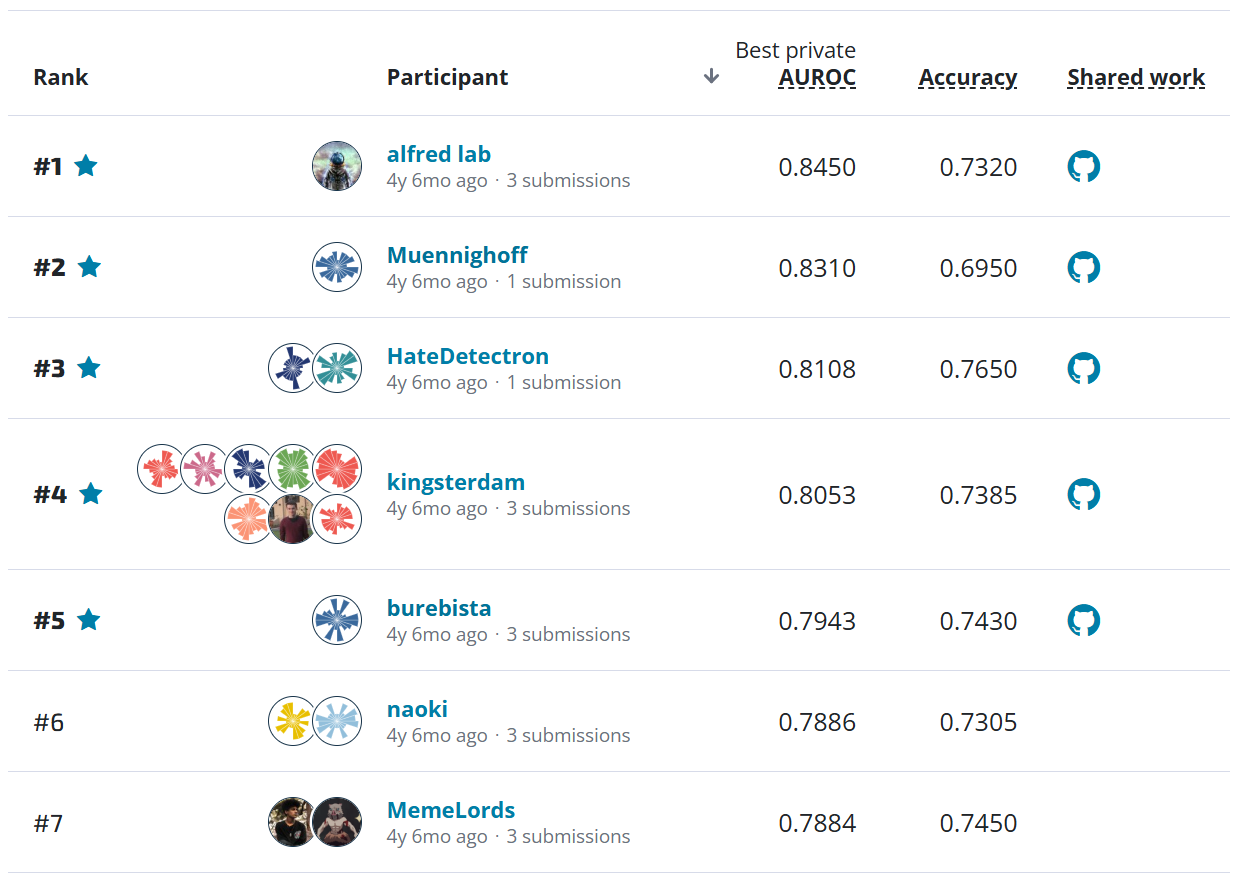
How to estimate surface-level NO2 using OMI column NO2 data¶

Welcome to the getting started notebook for the trace gas track of the NASA Airathon: Predict Air Quality challenge! The goal of this tutorial is to provide some helpful pointers and starter code to ingest, preprocess, explore, and work with one of the atmospheric data products derived from the Ozone Monitoring Instrument (OMI) onboard the Aura satellite. The specific scientific parameter covered by this tutorial is Tropospheric Column Nitrogen Dioxide (NO2), made available in Hierarchical Data Format (HDF). If OMI, NO2, or HDF are new concepts to you, then read on!

Before getting started, check out the Airathon competition homepage to learn more about the goal of this important challenge. In this tutorial, we'll:

• Provide an overview of some key concepts
• Explore the competition metadata
• Demonstrate how to load data in HDF5
• Clean and align OMI data
  • vector approach
  • raster approach
• Build a rudimentary model to predict trace gas levels

Let's get started!

The Data¶

What is OMI?¶

Aura is a multi-national NASA scientific research satellite that orbits the Earth to study Earth's ozone layer, air quality, and climate. Launched in 2004, it passes from south to north over the equator in the afternoon and is a member of a constellation of satellites with different science objectives that fly in close proximity known as the "A-Train". Their orbits are sun-synchronous, meaning that they pass the equator at the same local solar time on every orbit.

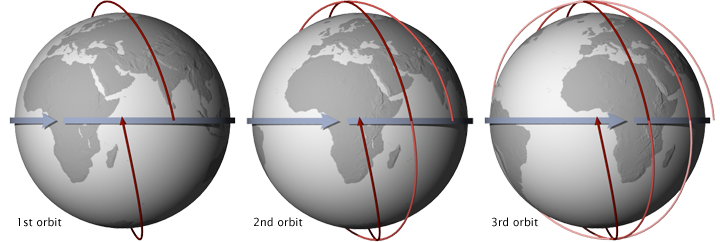
OMI is the name of a remote sensing instrument administered by NASA aboard the Aura satellite. This down-looking instrument measures backscattered sunlight in the visible and ultraviolet wavelengths and captures most of the Earth's surface each day. It tracks pollutants that threaten human health and agricultural productivity, and has ability to distinguish between aerosol types, such as smoke, dust, and sulfates. OMI can also measure cloud pressure and coverage, which are used to derive ozone. Sophisticated retrieval algorithms are used to convert measured radiation to pollution concentrations.

This exercise will focus on the OMNO2d Version 3 gridded 0.25 degree x 0.25 degree Level 3 product, which is pre-approved for the competition. Level 3 products represent values that have been filtered, pre-processed, and aggregated across different dates or footprints. 0.25 degree x 0.25 degree represents the resolution.

What is Tropospheric Column NO2?¶

OMNO2d reports Total and Tropospheric Column NO2. Nitrogen dioxide (NO2) is a harmful pollutant produced during combustion. According to NASA, it has been designated as a criteria pollutant by the U.S. Environmental Protection Agency (EPA) because of its negative effects on human health and the environment. Vertical column density (VCD) refers to the number of molecules between a remote sensing instrument and the Earth's surface. For NO2, the amount high in the atmosphere (in the stratosphere) is often removed to derive the column in the lower part of the atmosphere (in the troposphere), known as Tropospheric Vertical Column Density (TVCD). VCD and TVCD are typically measured in molecules of NO2 per square centimeter, and may be divided by 10¹⁵ for readability. These column densities have been found to be helpful for estimating surface-level NO2 levels.

While the OMNO2d data product contains a variety of data fields, we will focus on ColumnAmountNO2Trop. You are encouraged to explore and leverage all of the data fields made available by this data product using the OMI Data User's Guide.

Data loading¶

What's in our metadata?¶

First, let's organize our local repository using Cookiecutter Datascience and download the grid_metadata.csv, no2_satellite_metadata.csv, submission_format.csv, and train_labels.csv files from the data download page to our data/raw folder.

$ tree data/
data/
├── external
├── interim
├── processed
└── raw
    ├── grid_metadata.csv
    ├── no2_satellite_metadata.csv
    ├── submission_format.csv
    └── train_labels.csv

4 directories, 4 files

Next, let's import some handy tools for working with geospatial data and load the metadata to see what we have.

Satellite metadata¶

Our trace gas track satellite metadata file contains information about OMI and TROPOMI data made available for model training and testing. Let's create and inspect a subset of the OMI training data.

As OMI sweeps along an orbit, it collects data that is sectioned into pieces called granules. Each OMI granule contains Total Column NO2 and Total Tropospheric Column NO2 for all atmospheric conditions and for sky conditions where cloud fraction is less than 30 percent across each pixel. A single granule has a size of 720 x 1440 pixels. Each granule is identified by a unique granule_id with the following naming convention: {time_end}_{product}_{location}_{number}.hdf, where time_end is formatted as YYYYMMDDHHmmss. When locations and times have more than one associated file, this is denoted by number. For additional information about each of these fields, check out the NO2 data download instructions.

We can see that there are 671 OMI files to use for training. Each file covers the Los Angeles South Coast Air Basin, Delhi, and Taipei, denoted by dl-la-tpe.

Let's take a look at the time distribution in our training data.

We have a roughly balanced distribution of files across years (2019-2020) and months, with the fewest granules from the months of November and December.

Note that a single granule contains data that was captured within a 24 hour time window. For each location, OMI makes its observations mid-day.

Grid metadata¶

Next, let's take a look our grid cell metadata.

Each grid cell has a 5-character alphanumeric grid_id that uniquely identifies a 5 x 5 km grid cell and is associated with an observation in our train or test set. This file also contains important location and timezone (tz) information that can be used to localize dates, along with the polygonal coordinates of the grid cell. There is metadata available for 68 grid cells.

How do I load a OMI HDF5 file?¶

Our OMI data is stored in a HDF5 file format. At its lowest level, Hierarchical Data Format (HDF) is a set of file formats (HDF4 and HDF5) designed to store and organize large amounts of scientific data. HDF5 is the newer version of the format and is actively supported by a non-profit corporation called The HDF Group. This file format supports different data models, including multidimensional arrays, raster images, and tables. A single HDF file can hold a mix of related objects that can be accessed as a group or as individual objects.

In Python, we can read in HDF5 files using one of three libraries:

1. GDAL
2. PyTables
3. h5py

For this example, we'll be using h5py and code adapted from a script on the HDFEOS zoo.

The File module of the h5py package supports scientific datasets. Let's import this module along with some helpful tools to get started.

The OMI metadata file contains the locations of each OMI HDF5 file on s3. We can use the S3Path class from the cloudpathlib package to generate a path to a sample data file.

To read this file, we can instantiate a File object using a string representation of our path. Note that calling fspath downloads the file locally to a temporary directory.

Groups are the container mechanism by which HDF5 files are organized. They operate somewhat like dictionaries, where "keys" (Group objects) denote names of group members and "values" (Dataset objects) are the members themselves. The NO2 data we are interested in is contained in the HDFEOS group within the hdf object.

The File.visititems method allows us to recursively visit all items in a group. Let's use this method to explore the structure of our file.

Our hdf object contains four main variables listed under the Data Fields subtree:

• ColumnAmountNO2: total NO2 column density
• ColumnAmountNO2CloudScreened: total NO2 column density where cloud fraction is less than 30%
• ColumnAmountNO2Trop: column density of NO2 in the tropospheric layer
• ColumnAmountNO2TropCloudScreened: column density of NO2 in the tropospheric layer where cloud fraction is less than 30%

For more information about each of these variables, see this helpful Fact Sheet. For this tutorial, we will focus on the ColumnAmountNO2Trop variable. To access the ColumnAmountNO2Trop raw data, we can use [:] to create a copy of the dataset in memory.

According to our raw values, a single swath of our Tropospheric Column NO2 data contains 720 x 1440 pixels that represent averaged values across approximately 14 orbits in a single day. Given that our NO2 data covers the entire globe and our data has a resolution of 0.25 x 0.25 degrees, this shape is to be expected:

• Given latitude bounds of [-90, 90], 180 / 0.25 = 720 pixels
• Given longitude bounds of [-180, 180], 360 / 0.25 = 1440 pixels

Data processing¶

Now that we have our raw data, let's calibrate and map NO2 values to the competition grid cells.

How do I calibrate NO2 data?¶

To work with this data, we'll need to calibrate raw values by applying a set of accompanying attributes:

1. remove missing data
2. remove any remaining negative values
3. remove the offset and multiply by the scale factor (if applicable)
4. cast the data to a numpy masked array to handle missing entries

We can save these dataset attributes to a calibration dictionary using attrs on the trop_NO2 object.

Scale factors and offsets are simply used to optimize data storage. In this specific case, scaling by a factor of one and adjusting by an offset of zero won't result in any changes to the values.

Missing data denotes low quality readings. This can happen for a number of reasons, including cloud cover. We'll convert missing data to nans.

How do I align NO2 data with coordinates?¶

We can now align each corrected NO2 pixel with grid coordinates. From there, we will be able to determine which NO2 readings overlap with our training grid cells.

We will follow four steps to map values in a 2-dimensional matrix to 3-dimensional "world" coordinates. This process is known as georeferencing:

1. identify the original coordinate reference system (CRS) of the dataset
2. define reference points on our grid
3. perform any necessary reprojections of these points
4. connect points to NO2 values

We can choose to use one of two georeferencing approaches: vector- or raster-based. You may choose to use one or the other based on computational performance, memory usage, and/or library preferences.

Vector data is composed of discrete geometric locations, or vertices, that define the shape of a spatial object (e.g. points, lines, or polygons). Each feature can carry multiple attributes about a location. Geospatial vector data can be used with the convenient geopandas.GeoDataFrame class.

Raster data is stored as a grid of values that are rendered on a map as pixels, where each pixel value represents an area on the Earth's surface. Raster data is useful for representing continuous surfaces at high levels of detail and for performing efficient geometric computations. Rasters are commonly saved as GeoTIFFs, which contain geographic metadata.

Vector-based approach¶

Step 1: A CRS defines the mathematical approach used to transform real locations on the Earth into a flattened map. The CRS of our data is the latitude-longitude projection called WGS 84, also known as EPSG:4326. WGS 84 is the most common CRS in the world and is a standard among GPS datasets.

Step 2: Since the OMI Level 3 NO2 product represents global data, the bounds for latitude are [-90, 90] and the bounds for longitude are [-180, 180]. Given the 0.25 x 0.25 degree resolution of the data, we can create equispaced arrays at a 0.25 interval maintaining the bounds of the latitude and longitude.

Step 3: To determine which NO2 readings overlap with our training grid cells, we'll want to work in a consistent CRS. Luckily, the CRS of the competition grid cells is also WGS 84, so we won't need to reproject either set of coordinates.

Step 4: Finally, we can connect each NO2 value with a specific latitude and longitude by flattening our data into a GeoDataFrame of non-missing values. Each row represents a pixel value at a specific time and location. An OMI granule can contain up to 720 x 1440 rows. Our helper function, convert_array_to_df, will allow us to repeat this process for any data. Notice that we've added an additional keyword argument, total_bounds. Later on, this will allow us to optimize our operations by filtering out irrelevant points. For now, let's take a look at the entire dataset.

Notice that our dataframe contains over 500 thousand values. Let's plot the data using matplotlib.

Note that white pixels represent missing data.

Raster-based approach¶

Steps 1-3: Again, the CRS of our data is WGS 84 or EPSG:4326. Since NO2 represents global data, the bounds for latitude are [-90, 90] and the bounds for longitude are [-180, 180]. Since the CRS of the competition grid cells is WGS 84, we won't need to reproject either set of coordinates.

Step 4: We can define a matrix called an affine transformation that will allow us to transform image coordinates to real-world latitude and longitude coordinates. An affine transformation is a named tuple with elements a, b, c, d, e, f, which correspond to the elements in the matrix equation below, in which a pixel's image coordinates are x, y and its world coordinates are x', y'.

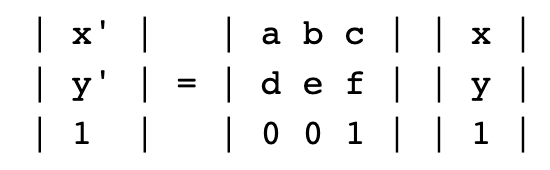
The only parameters we'll need are the bounds and resolution of our data file. We'll use rasterio.transform.from_bounds helper function to compute the matrix product of a translation and a scaling, which is the underlying formula to calculate this transformation matrix.

Putting this all together, we can write out a GeoTIFF file that holds our values, data type, missing data value, shape, and the coordinates of each point described by transform_wgs84.

Note: while it may be computationally advantageous to take the raster-based approach to data alignment, you'll want to experiment with different fill values, reprojections, and resampling methods if you decide to follow a raster-based approach. This tutorial is a good starting point.

Create and save feature data¶

We now have everything we need to iterate through our training files, calibrate and align NO2 values, mask the images to the extent of our grid cell bounds, and prepare our new training features.

Our training data contains up to 66 unique grid cells. Using geopandas, we can transform our grid cell metadata into a GeoDataFrame where each observation represents a Polygon geometry.

Since the OMI data are sparse, it is expected that many values will not overlap our grid cells. We can use the spatial join sjoin_nearest function from geopandas to identify the nearest non-null NO2 value to each grid cell.

But first, let's do some optimization. Remember that our gdf contains nearly 500 thousand points. Because the granule covers a much larger swath of land than our geographies of interest, the vast majority of those points will be irrelevant. For each city, we can generate a bounding box using the total_bounds attribute of our grid cell GeoDataFrame. We can then filter out points outside of the bounding box with the cx GeoDataFrame method. You may have noticed that in our convert_array_to_df helper function, we added a parameter that allows us to remove points outside of location bounds. By removing these points, we can dramatically speed up spatial joins!

We're now ready to use a subset of our previously generated gdf to identify points that are close to our training grid cells in a location, such as Los Angeles, and can compute the average Tropospheric Column NO2 per cell.

It's time to pull everything together! As a reminder, we've already created the following helper functions:

• calibrate_data
• define_coordinates
• convert_array_to_df

We'll add a helper function to create_calibration_dict.

As an example, we'll write a GeoDataframe that contains NO2 values for all points in our grid cells for which we have available Tropospheric Column NO2 data. To speed things up, we can parallelize this process using pqdm. Because we have granules that cover a range of times and locations, we expect the number of images per grid cell to vary.

Keep in mind, this represents just one of many approaches to using the satellite data for estimating surface-level NO2.

For example, you may choose to save out rasters cropped to the extent of the competition grid cells, compute a set of zonal statistics, or may want to include values from other datasets like ColumnAmountNO2 as additional image layers.

train_gdf describes 26,403 Tropospheric Column NO2 values near our competition training grid cells!

Simple benchmark model¶

Using train_df, let's prepare an extremely simple benchmark solution for the Airathon trace gas track.

We do not want to overstate our model's performance by overfitting to one or more dates or locations. To be sure that our method is sufficiently generalizable, let's set aside a portion of the data to validate the model. To ensure that we are not using data collected in the future to estimate prior NO2, we can subset the training data into training and validation sets using the datetime field.

In scikit-learn, we can set up a random forest with a few lines of code.

Finally, let's make predictions for the competition test set and save them to the submission format. To keep things simple, we'll impute missing features using the average NO2 value from the training data.

Finally, we will save our submission locally.

We can now head to the competition submissions page and upload our submission to obtain our model's R².

We should see an R² of -0.1543 on the leaderboard. Now it's up to you to make improvements and increase this score! We hope this tutorial provides a helpful framework for loading and exploring the data, correcting and aligning values, and working with geospatial vector and raster data.

Head over to the challenge homepage to get started. We can't wait to see what you build!

Banner image, artist's rendering of Aura, courtesy of NASA